5.
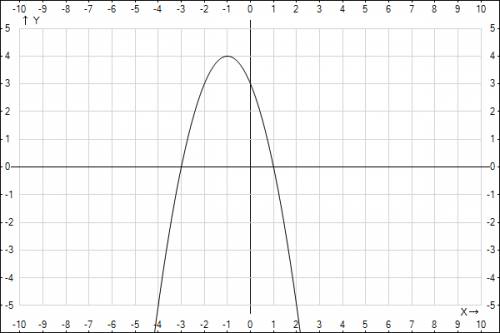
y=-x^2-2x+3,
a=-1<0 - ветви параболы вниз;
x_0=-b/(2a)=-(-2)/(2*(-1))=-1,
y_0=-(-1)^2-2*(-1)+3=4,
(-1;4) - вершина параболы;
x=0, y=3,
(0;3) - пересечение с Оу,
y=0, -x^2-2x+3=0,
x^2+2x-3=0,
по теореме Виета x_1=-3, x_2=1,
(-3;0), (1;0) - пересечения с Оx;
1) E_y=(-∞;4);
2) x∈(-1;+∞);
6.
(х^2+2х+1)(х^2-6х-16)<0,
(х^2+2х+1)(х^2-6х-16)=0,
х^2+2х+1=0, (x+1)^2=0, x+1=0, x=-1;
х^2-6х-16=0, по теореме Виета x_1=-2, x_2=8; х^2-6х-16=(x+2)(x-8);
(x+1)^2(x+2)(x-8)<0,
(x+1)^2≥0, x∈R,
(x+2)(x-8)<0,
-2<x<8,
x∈(-2;8);
7.
x^2-6bx+3b=0,
D<0,
D/4=k^2-ac=(-3b)^2-3b=3b^2-3b=3b(b-1),
3b(b-1)<0,
3b(b-1)=0,
b_1=0, b_2=1,
0<b<1,
b∈(0;1);
8.
ΔABC, уг.C=90°, CE - высота, AE=16см, BE=9см;
AB=AE+BE (по свойству сложения отрезков),
AB=16+9=25см;
AC^2=AB*AE (катет есть среднее геометрическое гипотенузы и смежного сегмента),
AC^2=25*16=400, AC=20см,
BC^2=AB*BE=25*9=225, BC=15см,
P=AB+AC+BC=25+20+15=60см.
а) Сколько имеется различных освещения коридора, включая случай когда все лампочки не горят. Как видим, каждая лампочка имеет два состояния (горит/не горит). Т.к. лампочек три, то всего вариантов будет 2³ = 8. Все 8 вариантов представлены на рисунке.
б) Сколько имеется различных освещения, если известно что лампочки №1 и №2 горят или не горят одновременно? Когда лампочки №1 и №2 горят, то лампочка №3 либо горит, либо не горит (2 варианта). Точно также, когда лампочки №1 и №2 не горят, то лампочка №3 тоже либо горит, либо не горит (2 варианта). Итого, 4 варианта. Проверяем по рисунку.
в) Сколько имеется различных освещения, если известно что при горящей лампочке №3 лампочка №2 не горит?
По рисунку считаем варианты - их 6. Когда лампочка №3 горит, то лампочка №2 не горит (по условию), а у лампочки №1 есть 2 варианта - горит/не горит. Когда лампочка №3 не горит, то вариантов у оставшихся лампочек будет 2² = 4. Вот и получается 6 вариантов.
г) сколько имеется различных освещения коридора когда горит большинство лампочек? Т.е. нам надо сосчитать случаи, когда одновременно горят 2 и более лампочек. По рисунку высчитываем, что есть 4 варианта. Или считаем число сочетаний двух лампочек из трёх, плюс число сочетаний три лампочки из трёх.
Итак, 4 варианта.