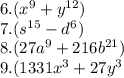
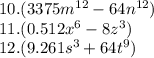

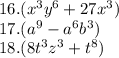

Найдем значение выражения 2 * ctg (pi/2 - 4 * a) * tg (pi/2 + 2 * a) * ctg (4 * a), если известно а = pi/6.
Подставим известное значение в само выражение и вычислим его значение. То есть получаем:
2 * ctg (pi/2 - 4 * a) * tg (pi/2 + 2 * a) * ctg (4 * a);
2 * ctg (pi/2 - 4 * pi/6) * tg (pi/2 + 2 * pi/6) * ctg (4 * pi/6);
2 * ctg (pi/2 - 2 * pi/3) * tg (pi/2 + pi/3) * ctg (2 * pi/3);
2 * ctg ((3 * pi - 4 * pi)/6) * tg ((3 * pi + 2 * pi)/6) * ctg (2 * pi/3);
2 * ctg (-pi/6) * tg (5 * pi/6) * ctg (2 * pi/3);
-2 * ctg (pi/6) * tg (5 * pi/6) * ctg (2 * pi/3);
-2 * √3 * (-√3/3) * (-√3/3) = -2 * (√3/3) = -2 * √3/3.
Объяснение:
Найдем значение выражения 2 * ctg (pi/2 - 4 * a) * tg (pi/2 + 2 * a) * ctg (4 * a), если известно а = pi/6.
Подставим известное значение в само выражение и вычислим его значение. То есть получаем:
2 * ctg (pi/2 - 4 * a) * tg (pi/2 + 2 * a) * ctg (4 * a);
2 * ctg (pi/2 - 4 * pi/6) * tg (pi/2 + 2 * pi/6) * ctg (4 * pi/6);
2 * ctg (pi/2 - 2 * pi/3) * tg (pi/2 + pi/3) * ctg (2 * pi/3);
2 * ctg ((3 * pi - 4 * pi)/6) * tg ((3 * pi + 2 * pi)/6) * ctg (2 * pi/3);
2 * ctg (-pi/6) * tg (5 * pi/6) * ctg (2 * pi/3);
-2 * ctg (pi/6) * tg (5 * pi/6) * ctg (2 * pi/3);
-2 * √3 * (-√3/3) * (-√3/3) = -2 * (√3/3) = -2 * √3/3.