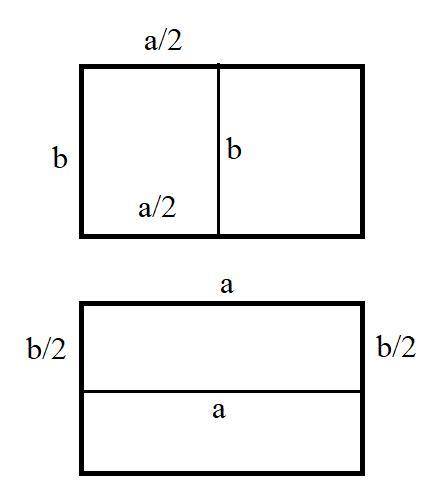
Пусть одна сторона прямоугольника a, другая b.
Так как прямоугольники , полученные у Коли и Миши после разрезания имеют равные периметры , значит прямоугольники равны
Пусть Коля разрезал сторону а пополам, а Миша сторону b ( cм. рис.)
Тогда периметр прямоугольника у Коли:
Р₁=(a/2)+b+(a/2)+b=a+2b
a+2b=17
Р₂=a+(b/2)+b+(b/2)=2a+b
2a+b=22
Решаем систему уравнений:
{a+2b=17 ⇒ a=17-2b
{2a+b=22
{ a=17-2b
{2·(17-2b)+b=22 ⇒ 34-4b+b=22 ⇒ 34-22=4b-b
3b=12
b=4
2a=22-b
2a=22-4
2a=18
a=9
О т в е т. P=2a+2b=2(a+b)=2(9+4)=26
Миша и Лера пришли в магазин за чаем. Мишиных денег хватает на три четверти пачки, Лере, если бы у нее было на 90 рублей больше, хватило бы на половину пачки. При этом известно, что у Миши на 70% больше денег, чем у Леры. Сколько стоит пачка чая ?
ответ: 1530 рублей
Объяснение: Допустим пачка чая стоит x рублей
3/4 пачки чая стоит 3x/4 ⇒ Миша имеет 3x/4 рублей
у Леры y рублей ⇒ Лере y = x/2- 90
Можно составить систему уравнений :
{ 3x/4 = y + y*70/100 { 3x/4 =1,7 y { 3x/4 = 1,7( x/2 - 90)
{ y = x/2 - 90 { y = x/2 - 90 { y = x/2 - 90 .
3x/4 =1,7( x/2 - 90) ⇔ 0,75x = 0,85x -153 ⇔ 153 = 0,85x -075x⇒
x = 1530 (рублей) .
Объяснение:
4.
(√х +5)/(х-25)=(√х +5)/((√х -5)(√х+5))=1/(√х-5)
(√3 -3)/(√5 -√15)=(√3 •(1-√3))/(√5 •(1-√3))=√(3/5)=√0,6
(х-2√(5х) +5)/(х-5)=((√х -√5)^2)/((√х -√5)(√х +√5))=(√х -√5)/(√х +√5)
5.
5/√15=(5√15)/15=√15/3=√(5/3)
5/(3√10)/=(5√10)/(3•10)=(√10)/6=√(5/18)
8/(√6 +√2)=(8(√6 -√2))/((√6 +√2)(√6 -√2))=(8(√6 -√2))/(6-2)=2(√6 -√2)=√24 -√8 или 2√2 •(√3 -1)
6.
При a≤0: √(3a^2)=-a√3
При a≥0: √(12a^6)=√(3•4(a^3)^2)=2a^3 •√3
При n>0: √(-m^3n^6)=пустое множество.