 и
и 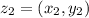 .
.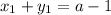
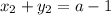
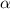 :
: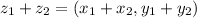
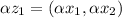
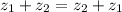 ). Очевидно, это выполняется исходя из того, как определена операция сложения.
). Очевидно, это выполняется исходя из того, как определена операция сложения.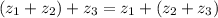 ) Выполняется всегда. Чтобы убедиться, возьмите третью пару этого множества и произведите сложение по определению.
) Выполняется всегда. Чтобы убедиться, возьмите третью пару этого множества и произведите сложение по определению.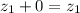 . Здесь под нулём я имел в виду не число 0, а элемент линейного пространства, обладающий такими свойствами.
. Здесь под нулём я имел в виду не число 0, а элемент линейного пространства, обладающий такими свойствами. 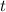 справедливо
справедливо 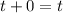 . Поэтому
. Поэтому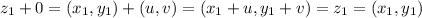
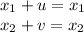
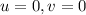
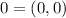
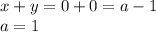
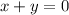 , то есть
, то есть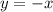
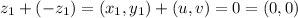
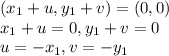
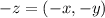
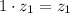
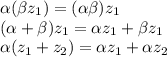
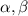 полагаются действительными, а пары чисел - любые.
полагаются действительными, а пары чисел - любые. 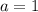 наше множество - действительно является линейным пространством.
наше множество - действительно является линейным пространством.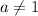 оно уже таковым не является. Для этого возьмите любую пару чисел
оно уже таковым не является. Для этого возьмите любую пару чисел 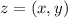 . Теперь умножим вектор на число
. Теперь умножим вектор на число 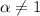 ,
,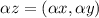 . Тогда его координаты должны удовлетворять указанному в условии сотношению
. Тогда его координаты должны удовлетворять указанному в условии сотношению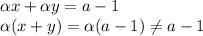 ни при каком а.
ни при каком а.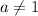 указанное множество уже теряет свойства линейного пространства.
указанное множество уже теряет свойства линейного пространства.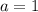
тогда
1/20 - это объём работы, которую выполняют за 1 час Игорь и Паша, работая вдвоём.
1/24 - это объём работы, которую выполняют за 1 час Паша и Володя, работая вдвоём
1/30 - это объём работы, которую выполняют за 1 час Володя и Игорь, работая вдвоём
1/20 + 1/24 + 1/30 = 6/120 + 5/120 + 4/120 = 15/120 = 1/8 - это УДВОЕННЫЙ объём работы, которую выполняют за 1 час Игорь, Паша и Володя, работая втроём.
1/8 : 2 = 1/16 - это объём работы, которую выполняют за 1 час Игорь, Паша и Володя, работая втроём.
А теперь весь объём работы 1, делим на 1/16 объём работы за 1 час и получаем искомое время.
1 : 1/16 = 1 * 16/1 = 16 час
ответ: 16 час = 960 мин ( этот ответ при условии, что на покраску забора ушло громадное количество 20 час, 24 час, 30 час
А если в условии ошибочно дано время в Часах, то при решении и в ответе берём минуты, т.е. 20 мин, 24 мин, 30 мин, тогда ответ: 16 мин.