846875
Объяснение:
Всего 6-значных чисел 900000: на первое место можно поставить одну из 9 цифр, на оставшиеся - любую из 10.
Посчитаем, у скольких чисел произведение цифр не делится на 4. Такое бывает в двух случаях:
Произведение цифр нечётное, тогда все цифры нечётные, на каждое место можно независимо выбирать один из 5 вариантов цифры. Таких чисел Произведение цифр делится на 2, но не на 4, тогда в числе одна из цифр 2 или 6, а остальные - нечетные. Выбрать место для четной цифры можно а после этого расставить цифры -
Произведение цифр делится на 2, но не на 4, тогда в числе одна из цифр 2 или 6, а остальные - нечетные. Выбрать место для четной цифры можно а после этого расставить цифры - 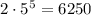 Всего получаем
Всего получаем 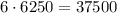 чисел.
чисел.Общее количество чисел, произведение цифр которых не делится на 4, равно  , значит, искомое количество равно
, значит, искомое количество равно 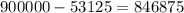
При каких значениях a неравенство имеет не менее пяти целочисленных решений х²+у²-а²≤6х-4у+а-13.
Объяснение:
х²+у²-а²≤6х-4у+а-13 ,
х²-6х+у²+4у≤а²+а-13 ,
х²-6х+9-9+у²+4у+4-4≤а²+а-13 , свернем формулы
(х-3)²+(у+2)²≤а²+а-13 +13 ,
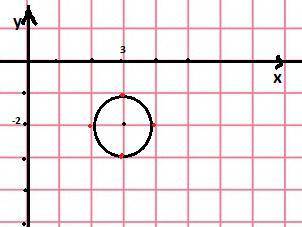
(х-3)²+(у+2)²≤а²+а . Данное неравенство ограничивает часть плоскости внутри круга с центром (3;-2) . Если r=1 , то целочисленных решений пять ( четыре лежат на окружности и одно в центре) . Значит радиус r≥1 или r²≥1.
Выражение а²+а =r² и тогда а²+а≥1 , а²+а-1≥0 . Нулями данного квадратного трехчлена являются значения :
а₁=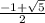 , а₂=
, а₂=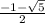 . Метод интервалов :
. Метод интервалов :
+++++++[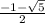 ]- - - - - -[
]- - - - - -[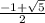 ]+++++++. ⇒
]+++++++. ⇒
х∈(-∞ ;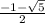 ] и [
] и [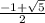 ; +∞).
; +∞).
держи