И так распишем модуль по определению.
Так программа не позволяет записывать большие уравнения буду делать по частям, а потом всё объединять.
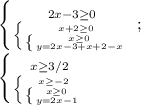
1. x≥3/2, y=2x-1
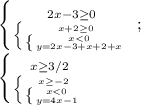
У этой системы нет пересечения.
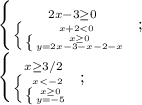
У этой системы нет пересечения.
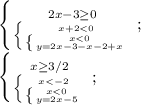
У этой системы нет пересечения.
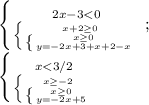
2. 0≤x<3/2, y=-2x+5
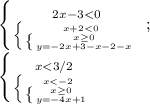
У этой системы нет пересечения.
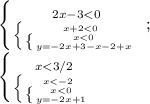
3. x<-2, y=-2x+1
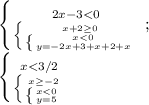
4. -2≤x<0, y=5
Я перебрал все возможные случаи раскрытия модулей теперь посмотрим прерываются ли эти графики.
1. x≥3/2, y=2x-1;
2. 0≤x<3/2, y=-2x+5;
3. x<-2, y=-2x+1;
4. -2≤x<0, y=5.
f1(3/2)=3*2/2-1=2 и f2(3/2)=-2*3/2+5= -3+5=2 Эти концы сходятся.
f2(0)= -2*0+5=5 и f4(0)=5 сходятся
f4(-2)=5 и f3(-2)= -2*(-2)+1=4+1=5 сходятся.
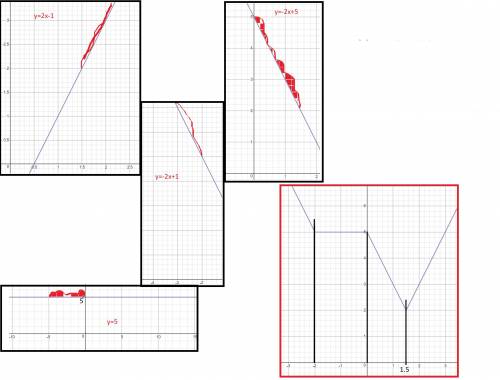
Далее рисуем каждый график отдельно отмечай необходимый нам интервал и переносим всё на один график. См. график внизу
x=-1/13
2) -2x²=2
x²=-1
нет решений(если на уровне 8 класса)
3)4,5х=0
х=0
4)х²-3х=0
х(х-3)=0
х[1]=0 или х[2]=3
5)4х²-12=0
4(х²-3)=0 /:4
х²=3
х=+√3; -√3
6)х²=49
х=+7; -7
7)х²=-16
нет решений(опять же, на уровне 8 класса)
8)х²=0
х=0
9)х²=1
х=+1; -1
10) х²-5х много, решу через теорему Виета)
ВИЕТА
нам известна формула для приведенного уравнения вида х²+рх+q=0:
х[1]+х[2]=-p
x[1]×x[2]=q
в нашем уравнении х²-5х+6=0
-p=5
} =›
q=6
решаем систему:
x[1]+x[2]=5
x[1]×x[2]=6
ОТВЕТ:х[1]=2; х[2]=3
11) х²-2х-3=0(это уравнение решу через дискриминант)
в уравнении вида ax²+bx+c=0
D=b²-4ac
a=1
b=-2
c=-3
D=4-4×(-3)=16
х[1]=(-b-√D)/2a=-1
х[2]=(-b+√D)/2a=3
P.S. икс один, икс два писала в крадратных скобках, потому что на телефоне не нашла нижние индексы
P.P.S. расписывать так не нужно, просто я писала, чтоб понятней было