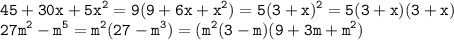
45+30x+5x^2=5(9+6x+x^2)=5(3+x)^2
27m^2-m^5=m^2*(27-m^3)=m^2*(3-m)*(9+3m+m^2)
1) х² - 8х + 15 ≥ 0
Решаем уравнение
х² - 8х + 15 = 0
D = 8² - 4 · 15 = 4 = 2²
x₁ = 0.5(8 - 2) = 3
x₂ = 0.5( 8 + 2) = 5
Значения функции у = х² - 8х + 15 не отрицательны при х≤ х₁ и х≥ х₂
Неравенство имеет решение при х ∈ (-∞; 3] ∪ [5; +∞)
2) х² - 6х + 9 < 0
Преобразуем левую часть неравенства
(х - 3)² < 0
Квадрат любого числа неотрицателен, поэтому неравенство не имеет решений.
3) х² - 4х + 20 ≤ 0
Решаем уравнение
х² - 4х + 20 = 0
D = 4² - 4 · 20 = -64
Уравнение решений не имеет. Поэтому все значения функции у = х² - 4х + 20 положительны, и неравенство не имеет решений.
4) -х² + 7х - 12 < 0
Решаем уравнение
-х² + 7х - 12 = 0
D = 7² - 4 · 12 = 1
x₁ = -0.5(-7 + 1) = 3
x₂ = -0.5(-7 - 1) = 4
Значения функции у = -х² + 7х - 12 отрицательны при х > х₁ и х < х₂
Неравенство имеет решение при х ∈ (3; 4)
F'(x) = f(x)
((x-1)²)' = 2(x-1)
Первообразная F(x) = (x-1)²+c - общий вид
у=2(х-1) = 2х-2 - график прямая
1. чертим систему координат; отмечаем начало координат - точку О (0; 0), отмечаем стрелками положительное направление: вправо и вверх; подписываем оси : вправо - х, вверх - у; отмечаем единичные отрезки по каждой оси в 1 клетку.
2) для построения прямой достаточно двух точек, занесем их координату в таблицу:
х= 0 2
у= -2 2
3) отметим точки (0; -2) и (2; 2) на координатной плоскости; проведем через данные точки прямую линию; подпишем график функции у= 2х-2
Всё!