192
Объяснение:
Чётные цифры: 0, 2, 4, 6, 8.
пятизначные числа не начинаются с 0, значит, на первом месте любая из четырёх цифр: 2, 4, 6, 8 На втором месте цифра 1 или 3, два варианта.
На третьем месте можно написать 0, но нельзя ту цифру, которая на первом месте. Цифры в записи числа не должны повторяться. Значит, четыре варианта для записи второй цифры.
На четвёртом месте цифра 5 или 7 - два варианта.
На пятом месте - чётная цифра, но не такая, как на первом и третьем - три варианта.
На шестом месте цифра 9 - один вариант.
По правилу произведения перемножаем возможные варианты постановки каждой цифры:
4⋅2⋅4⋅2⋅3⋅1=192
ответ: 192
192
Объяснение:
Чётные цифры: 0, 2, 4, 6, 8.
пятизначные числа не начинаются с 0, значит, на первом месте любая из четырёх цифр: 2, 4, 6, 8 На втором месте цифра 1 или 3, два варианта.
На третьем месте можно написать 0, но нельзя ту цифру, которая на первом месте. Цифры в записи числа не должны повторяться. Значит, четыре варианта для записи второй цифры.
На четвёртом месте цифра 5 или 7 - два варианта.
На пятом месте - чётная цифра, но не такая, как на первом и третьем - три варианта.
На шестом месте цифра 9 - один вариант.
По правилу произведения перемножаем возможные варианты постановки каждой цифры:
4⋅2⋅4⋅2⋅3⋅1=192
ответ: 192
Нули функции:
Согласно теореме Виета, имеем:
По условию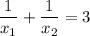 или
или 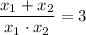 .
.
Следовательно, подставляя значения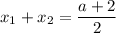 и
и 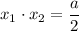 , найдем параметр
, найдем параметр  :
:
Таким образом,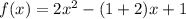 , то есть
, то есть 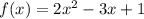
Найдем координаты точки вершины параболы:
Значит,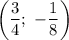 — точка вершины параболы.
— точка вершины параболы.
Найдем точки пересечения с осями координат:
а) С осью абсцисс:
Следовательно,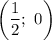 и
и 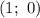 — точки пересечения функции с осью абсцисс.
— точки пересечения функции с осью абсцисс.
б) С осью ординат:
Следовательно,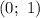 — точка пересечения с осью ординат.
— точка пересечения с осью ординат.
Согласно свойству симметрии параболы,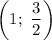 — точка графика.
— точка графика.
Изобразим график данной функции (см. вложение).
Нули функции:
Согласно теореме Виета, имеем:
По условию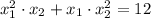
Следовательно, подставляя значения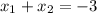 и
и 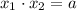 , найдем параметр
, найдем параметр  :
:
Таким образом,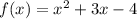
Найдем координаты точки вершины параболы:
Найдем точки пересечения с осями координат:
а) С осью абсцисс:
Следовательно,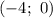 и
и 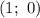 — точки пересечения функции с осью абсцисс.
— точки пересечения функции с осью абсцисс.
б) С осью ординат:
Следовательно,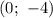 — точка пересечения с осью ординат.
— точка пересечения с осью ординат.
Согласно свойству симметрии параболы,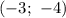 — точка графика.
— точка графика.
Изобразим график данной функции (см. вложение).