В задаче отсутствует вопрос. Исхожу из предположения, что требуется определить время движения. t = S/v = 400/v. Но скорость задана не конкретным значением, а границами. Значит время можно только оценить. 50<v<80 заменим обратными числами,при этом меняем знак неравенства. 1/50 > 1/v > 1/80. Запишем в привычном виде: 1/80 < 1/v < 1/50. Теперь умножим все части неравенства на 400. 400/80< 400/v< 400/50. 5< t<8. Значит при заданных условиях время движения от 5 до 8 часов.
1-ый случай, когда a>0, b>0, тогда точка A лежит в 1-ой координатной четверти. Следовательно, точка B лежит в 3-ей координатной четверти и не принадлежит графику функции y=x^2, так как это парабола, и обе ее ветви лежат в 1-ой и 2-ой к.четвертях. 2-ой случай, когда a>0, b<0, тогда точка A лежит в 4-ой координатной четверти. Этого не может быть, так как ветви параболы по условию находятся в 1 и 2-ой к.ч. 3-ий случай, когда a<0, b>0, тогда точка A лежит в 2-ой координатной четверти. Следовательно, точка B лежит в 4-ой координатной четверти и не принадлежит графику функции y=x^2. 4-ый случай, когда a<0, b<0, тогда точка A лежит в 3-ей к.ч. Этого не может быть, так как ветви параболы по условию находятся в 1 и 2-ой к.ч.
Если тебя не просят рассматривать случаи с различными знаками a и b, то доказательство идет другое. Координаты точки A имеют положительные знаки, отсюда следует, что она находится в первой координатной четверти. Координаты точки B имеют отрицательные знаки, отсюда следует, что она лежит в 3-ей координатной четверти, а значит, она не может принадлежать графику функции. Это будет отчетливо видно, если ты посмотришь на график этой функции.
Так как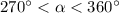
, то это угол 4 четверти. В 4 четверти тангенс отрицателен.