Question

решить задания , могли бы дать подробное решение. Благодарю.
1)Вычислить.
2)Сравнить выражения.
3)При каких значениях выражение а(альфа) возможно равенство.​

Answer 1

1. а) $2\cos30^{\circ}\cdot ctg 60^{\circ} - \sin\frac{3\pi}{2} = 2\cdot\frac{\sqrt{3}}{2}\cdot\frac{\sqrt{3}}{3} - \sin270^{\circ} = 1 - (-1) = 2$

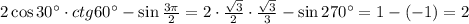
в данном пункте считаем по табличным значениям

б)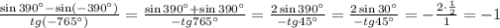 $\frac{\sin390^{\circ}-\sin(-390^{\circ})}{tg(-765^{\circ})}} = \frac{\sin390^{\circ}+\sin390^{\circ}}{-tg765^{\circ}}} = \frac{2\sin390^{\circ}}{-tg45^{\circ}}} = \frac{2\sin30^{\circ}}{-tg45^{\circ}}} = - \frac{2\cdot\frac{1}{2}}{1} = -1$

в данном пункте пользуемся непарностью синуса и тангенса (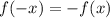$f(-x) = -f(x)$) и периодичностью (у синуса 360°, у тангенса - 180°)

2. а) Поскольку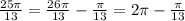 $\frac{25\pi}{13} = \frac{26\pi}{13} - \frac{\pi}{13} = 2\pi - \frac{\pi}{13}$, то это угол 4 чверти.

Аналогично выясняем что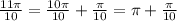 $\frac{11\pi}{10} = \frac{10\pi}{10} + \frac{\pi}{10} = \pi + \frac{\pi}{10}$- угол 3 чверти.

Поскольку косинус в 4 чверти и тангенс в 3 чверти имеют знак плюс, то и первое выражение >0.

$\sin(-330^{\circ}) = -\sin{330^{\circ}}$

330 градусов - угол 4 чверти, где синус отрицательный. Значит выражение выше будет >0 (- на - дает +).

100 градусов - угол второй чверти, котангенс же там отрицательный. Значит всё наше выражение <0.

Поэтому,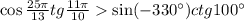 $\cos\frac{25\pi}{13}tg\frac{11\pi}{10} \sin(-330^{\circ})ctg100^{\circ}$

б) Так как π радиан - это 180 градусов, то 2 радиана будет углом второй чверти, поскольку 2 < 3,14 = π, но в то же время 2 > 1,57 = π/2.

Косинус второй чверти отрицательный, а косинус двух градусов положительный (угол 1 чверти).

Поэтому,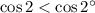 $\cos2$

3. $\sin x=a^2+1$

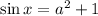
Выражение имеет смысл тогда, когда правая часть лежит в промежутке [-1;1] (область значений синуса).

Можем записать:$a^2+1 \in [-1;1] -1\leq a^2+1 \leq 1$

$\left \{ {{a^2+1\leq1} \atop {a^2+1 \geq -1}} \right. \\\left \{ {{a^2\leq0} \atop {a^2 \geq -2}} \right.$

Второе неравенство имеет смысл при всех действительных а, так как квадрат числа - неотрицательная величина. Выходя с этого, решением первого неравенства может быть лишь одно число: a = 0.

ответ: a = 0.