Пусть скорость до увеличения была х км/ч, тогда после увеличения стала (x+10) км/ч. Время пути поезда до увеличения скорости: 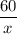 ч.
ч.
Время пути поезда после увеличения скорости: 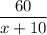 ч.
ч.
Известно, что поезд был задержан на станции на 12 мин = 12/60 ч = 1/5 ч
Составим уравнение:
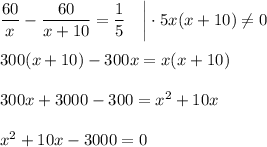
По т. Виета
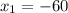 - не удовлетворяет условию;
- не удовлетворяет условию;
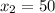 км/ч — скорость поезда до увеличения скорости (или первоначальная скорость)
км/ч — скорость поезда до увеличения скорости (или первоначальная скорость)
50 + 10 = 60 км/ч — скорость поезда после увеличения скорости(или новая скорость).
ответ: первоначальная скорость поезда равна 50 км/ч, а после новая скорость — 60 км/ч.
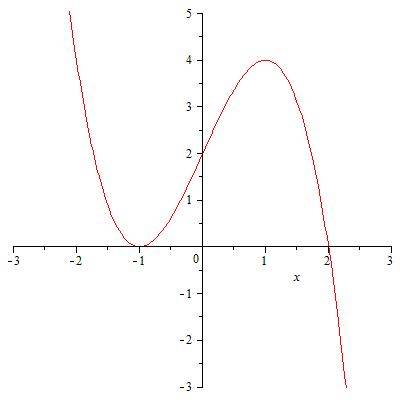
1) Уравнение касательной имеет вид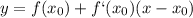
С этого уравнения видно, что коэффициент возле переменной является значением производной функции в точке касания. Найдём же эту точку.
Проведём проверку найденных корней:
Первый корень дал нам уравнение другой касательной,он нам не подходит
Мы нашли абсциссу точки прикосновения, это -2
ответ: х= -2
2) Нужно найти производную функции и приравнять её к нулю, чтобы проверить критические точки на наличие экстремума
Мы нашли стационарную точку х = 3.5 , проверим её на экстремум с метода интервалов.
Подставляю в нашу производную значения с интервалов (подставляем только в числитель, так как знаменатель всегда положителен и мы это доказали выше)
Получаем такие знаки на интервалах:
Видим, что производная при переходе через точку х = 3.5 меняет свой знак с минуса на плюс, что является достаточным условием существования минимума функции в данной точке.
ответ: х = 3.5 - точка минимума функции