натуральное число, тогда 
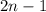будет натуральным и нечётным числом. Возведем данное число в квадрат: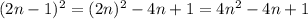
, 0 делиться на 8, следовательно условие выполняется.. Докажем что данное число делиться на 8 при 
:
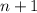делиться на 8. Следовательно, существует натуральный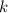 
так что: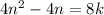
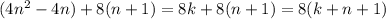следовательно, при 
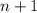данное число тоже делиться на 8. Ч.Т.Д.
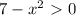
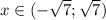. Только учитывая это, можно избавиться от знаменателя (работать будем с уравнением 
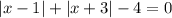), но на это нужно будет обращать внимание.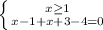
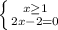
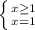- система подходит.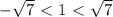
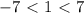- верно. Значит, 1 нам подходит.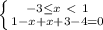
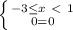- всякое решение из промежутка [-3; 1)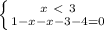
Объяснение:
sin x gfuv gch345 5758 7utr76