Используем метод неопределённых коэффициентов.Предположим, что левая часть уравнения разлагается на множители второй степени с целыми коэффициентами. Обозначим один из них через , другой - через .
Задача сводится к нахождению p, q, r, s. Тогда
Можно попробовать взять q=4, s=-2, тогда p=2, r=-2, а уравнение может быть представлено в виде:
не имеет действительных корней, так как дискриминант меньше 0 (2^2-4*4=-12).
Сумма корней:
если взять q=-4, s=2, тогда p=-2, r=2, а уравнение может быть представлено в виде:
не имеет действительных корней, так как дискриминант меньше 0 (2^2-4*2=-4).
Пусть скорость первой группы х км/ч, тогда скорость второй группы х+1 км/чКаждая из них шла по 2 часа.Первая х кмВторая х+1) кмВместе, идя навстречу друг другу, они км.Составим уравнение2х+2х+2=184х=16х=16:4=4 (км/ч) - скорость первой группы4+1=5 ( км/ч) - скорость второй группы.ответ: 4км/ч; км/ч ВТОРАЯ ЗАДАЧАЧА х-карандаши в 1 маленькой коробке х+12 карандаши в большой коробке 5*(х+12)=15*х 5*х+60=15*х 10*х=60 х=6 5*(6+12)=90 15*6=90 90+90=180 3 ЗАДАЧА (х+7)*2-10=20, 2х+14-10=20, 2х=16, х=8 ответ: число 8 ЕСЛИ НЕТРУДНО ТО ОТМЕТЬТЕ ЗА ЛУЧШИЙ :) :)
Используем метод неопределённых коэффициентов.Предположим, что левая часть уравнения разлагается на множители второй степени с целыми коэффициентами. Обозначим один из них через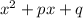
, другой - через 
.
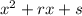Задача сводится к нахождению p, q, r, s. Тогда
Можно попробовать взять q=4, s=-2, тогда p=2, r=-2, а уравнение может быть представлено в виде:
Сумма корней: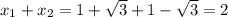
если взять q=-4, s=2, тогда p=-2, r=2, а уравнение может быть представлено в виде:
Сумма корней: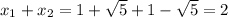
ответ: 2.