Question

1. Найдите первообразную F(x) для функции f(x)=2+sin4x, если F(п/4)= -3п. В ответе укажите значение F(7п/4)

2. Наибольшее значение первообразной F(x) для функции f(x)=e^x+2x+1 на отрезке [0;2] равно e^2. Найдите наименьшее значение первообразной на этом отрезке

3. График первообразной F(x) для функции f(x)= -6/x^2 на промежутке (-∞;0)проходит через точку (-2;-3). Решите уравнение F(x)=f(x). Если уравнение имеет более одного корня, в ответе запишите больший корень

Answer 1

$1. f(x)=2+\sin 4x\\\\F(x)=2x-\frac{\cos4x}{4}+C.\\\\F(\frac{\pi}{4})=-3\pi;\\\\ 2\cdot\frac{\pi}{4}-\frac{\cos\pi}{4}+c=-3\pi;\\\\\frac{\pi}{2}+\frac{1}{4}+c=-3\pi \\\\ C=-3\pi-\frac{\pi}{2}-\frac{1}{4}\\\\C=-\frac{7\pi}{2}-\frac{1}{4}$

Заданная первообразная -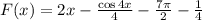 $F(x)=2x-\frac{\cos4x}{4}-\frac{7\pi}{2}-\frac{1}{4}$

$F(\frac{7\pi}{4})=2\cdot\frac{7\pi}{4}-\frac{\cos7\pi}{4}-\frac{7\pi}{2}-\frac{1}{4}=\frac{7\pi}{2}+\frac{1}{4}-\frac{7\pi}{2}-\frac{1}{4}=0.$

ОТВЕТ: 0.

$2. f(x)=e^x+2x+1, \max_{[0;2]}F(x)=e^2.\\\\F(x)=e^x+x^2+x+C.$

График данной первообразная вне зависимости от значения константы на заданном отрезке монотонно возрастает. Поэтому максимальное значение первообразная принимает на правом конце отрезка [0; 2] - т.е. при х = 2.

$F(2)=e^2+2^2+2+C=e^2+6+C=e^2;\\\\e^2+6+C=e^2\\\\6+C=0\Rightarrow C=-6.$

Заданная первообразная -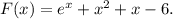 $F(x)=e^x+x^2+x-6.$

Соответственно все из того же факта монотонного возрастания следует и то, что минимальное значение первообразная принимает на левом конце отрезка [0; 2] - т.е. при х = 0.

$F(0)=e^0+0^2+0-6=1-6=-5.$

ОТВЕТ: -5.

$3. f(x)=-\frac{6}{x^2}=-6x^{-2}, x\in(-\infty; 0) \\\\F(x)=-6\cdot\frac{x^{-2+1}}{-2+1}+C=-6\cdot\frac{x^{-1}}{-1}+C=\frac{6}{x}+C.$

По условию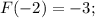 $F(-2)=-3;$

$\frac{6}{-2}+C=-3;\\\\ -3+C=-3\Rightarrow C=0.$

Заданная первообразная -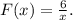 $F(x)=\frac{6}{x}.$

Решим уравнение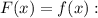 $F(x)=f(x):$

$\frac{6}{x}=-\frac{6}{x^2}, x\neq 0 \\\\ 6\cdot x^2=x\cdot-6;\\\\6x^2+6x=0;\\\\6x(x+1)=0\Rightarrow x_1=0, x_2=-1.$

Однако вспоминаем про ограничение для самой переменной: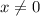 $x\neq 0$ (о чем прописано также и в условии существования первообразной). Делаем вывод: уравнение имеет единственное решение $x=-1$

ОТВЕТ: {-1}.