Основание логарифма больше 0 и не равно 1. А подлогарифмическое выражение должно быть больше 0.
Разберемся с последним неравенством.
Это неравенство легко решить методом интервалов. Найдем нули функции:
Отсюда вытекают 3 случая. (рассматривать случай при а от 0 до 1 нет смысла, так как область определения в это случае будет в границах от 0 до 1, и 4 целых чисел тут не наберется)
Первый случай: В этом случае при любых значениях а в рассматриваемом промежутке не будет 4 целых чисел в области определения.
Второй случай: При а = 5 вовсе не будет никакой области определения, так как
Третий случай: В этом случае можно выделить те значения а при которых область определения функции будет содержать ровно 4 целых числа.
1)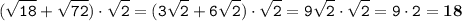
2)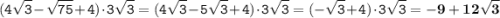
3)