
Рассмотрим функцию 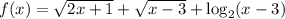 на её области определения
на её области определения 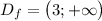
График этой функции пересечёт линию 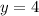 более одного раза только если будут существовать промежутки разной монотонности (на каких-то функция возрастает, на других - убывает).
более одного раза только если будут существовать промежутки разной монотонности (на каких-то функция возрастает, на других - убывает).
Обязательным условием смены монотонности функции является обращение её производной в ноль (или несуществование производной) в точке, где монотонность меняется. Попробуем их найти.
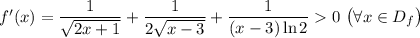
Как видно из вида производной, для всех точек области определения функции, она не обращается в ноль (более того, функция строго возрастает).
Таким образом, наше уравнение не может иметь более одного корня.
Методом пристального взгляда замечаем, что 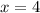 - корень уравнения.
- корень уравнения.
Действительно, 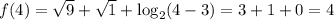
ответ. 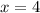
Вероятность выигрыша 0,5, значит вероятность проигрыша 1-0,5=0,5
Найти количество билетов чтобы вероятность выигрыша была
не менее 0,999
Решим альтернативную задачу: найдем количество билетов, чтобы вероятность проигрыша была менее 0,001
первый билет проиграл 0,5
значит берем второй билет и он тоже проиграл 0,5*0,5=0,25>0.001
значит берем третий билет и он тоже проиграл 0,25*0,5=0,125>0.001
четвертый 0,125*0,5=0,0625>0,001
пятый 0,0625*0,5=0,03125>0.001
шестой 0,03125*0,5=0,015625>0,001
седьмой 0,015625*0,5=0,0078125>0.001
восьмой 0.0078125*0.5=0.00390625>0,001
девятый 0,0039*0,5=0,00195>0.001
десятый 0.00195*0.5=0.00097 <0.001
Значит среди 10 билетов хотя бы один будет выигрышный