Пусть х столов с двумя ящиками и
у столов с тремя ящиками, тогда
(х+у) столов с одним ящиком
По условию всего 14 столов, получаем первое уравнение:
х+у+(х+у) = 14
По условию всего 25 ящиков, получаем второе уравнение:
1·(х+у) + 2·х + 3у = 25
Решаем систему:
{х+у+(х+у) = 14
{1·(х+у) + 2·х + 3у = 25
{2х+2у = 14
{х+у + 2х + 3у = 25
{2х+2у = 14
{3х+4у = 25
{x+y = 7
{3x+4y = 25
Из первого уравнения выразим х через у:
x=7-y
Подставим во второе и найдем у.
3·(7-y)+4y = 25
21-3y+4y = 25
y=25-21
y = 4 стола с тремя ящиками.
ответ: 4.
Задание № 1:
Найдите последнюю ненулевую цифру значения произведения 40^50*50^40?
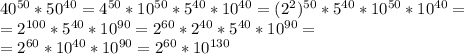
10^130 нас не интересует. Попробуем повозводить 2 в степень:
2^1=2, 2^2=4, 2^3=8, 2^4=16, 2^5=32
Пятая степень, как и первая, оканчивается на 2. Образуется своего рода цикл.
Чтобы узнать последнюю цифру степени N, нужно N разделить на 4. Остаток от деления соответствует степени, последняя цифра которой совпадает с последней цифрой степени N. Остаток 0 соответствует 4-ой степени.
60/4=15, остаток 0 – 4 степень оканчивается на 6, значит и 60 степень оканчивается на 6
ОТВЕТ: 6
Обозначим:
A(i) - игрок выиграл i-ю партию (вероятность этого события p = 1/2). ~A(i) - игрок проиграл i-ю партию (вероятность этого события q = 1 - p = 1/2).
P(m,N) - событие "игрок выиграл m партий из N".
S(m,N) - событие "игрок выиграл не менее m партий из N". s(m,N) - вероятность события "игрок выиграл не менее m партий из N"
C(k,N) = [N!/k!(N-k)!]*p^k*q^(N-k) - вероятность k выигрышей и N-k проигрышей в N партиях для каждого из игроков. C(k,N) = [N!/k!(N-k)!]*(1/2)^N, т.к. в нашем случае p = q = 1/2.
p(m,N) - вероятность события "игрок выиграл m партий из N": p(m,N) = C(m,N) = [N!/m!(N-m)!]*p^m*q^(N-m) = [N!/m!(N-m)!]*(1/2)^N
s(m,N) - вероятность события "игрок выиграл не менее m партий из N": s(m,N) = p(m,N) + p(m+1,N) +...+ p(N,N).
а)
p(1,2) = [2!/(1!1!)]*(1/2)^2 = 2*(1/4) = 1/2
p(2,4) = [4!/2!(2)!]*(1/2)^4 = 6*(1/2)^4 = 3/8
Следовательно, p(1,2) > p(2,4)
Вероятность выигрыша одной партии из двух больше, чем вероятность выигрыша двух партий из четырех.
б)
s(2,4) = p(2,4) + p(3,4) + p(4,4) = 3/8 + 1/4 + 1/16 = 11/16
s(3,5) = p(3,5) + p(4,5) + p(5,5) = 10/32 + 5/32 +1/32 = 1/2
Следовательно, s(2,4) > s(3,5)
Вероятность выигрыша не менее двух партий из четырех больше, чем вероятность выигрыша не менее трех партий из пяти.