В решении.
Объяснение:
Функцію задано формулою y = 1/4 * x. Знайдіть:
1) значення у, якщо x = 8; 2; -4; -3;
а) y = х/4; х = 8;
у = 8/4 = 2;
При х = 8 у = 2;
б) y = х/4; х = 2;
у = 2/4 = 0,5;
При х = 2 у = 0,5;
в) y = х/4; х = -4;
у = -4/4 = -1;
При х = -4 у = -1;
г) y = х/4; х = -3;
у = -3/4 = -0,75;
При х = -3 у = -0,75;
2) значення x,при якому y дорівнює -2; -1/4; 0; 16;
а) y = х/4; у = -2;
-2 = х/4
х = -2 * 4
х = -8;
у = -2 при х = -8;
б) y = х/4; у = -1/4;
-1/4 = х/4
х = -1/4 * 4
х = -1;
у = -1/4 при х = -1;
в) y = х/4; у = 0;
0 = х/4
х = 0 * 4
х = 0;
у = 0 при х = 0;
г) y = х/4; у = 16;
16 = х/4
х = 16 * 4
х = 64;
у = 16 при х = 64.
![lim_{x\to \infty }\frac{x+1}{x-2}=lim_{x\to \infty }\frac{\frac{x}{x}+\frac{1}{x}}{\frac{x}{x}-\frac{2}{x}}=lim\frac{1+\frac{1}{x}}{1-\frac{2}{x}}=[\frac{1+0}{1-0}]=\frac{1}{1}=1](/tpl/images/0237/6916/b2fde.png)
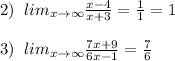
![lim_{x\to \infty }\frac{x+3}{5x^2+2x-5}=0,tak\; \; kak\\\\lim_{x\to \infty }\frac{\frac{x}{x^2}+\frac{3}{x^2}}{\frac{5x^2}{x^2}+\frac{2x}{x^2}-\frac{5}{x^2}}=lim\frac{\frac{1}{x}+\frac{3}{x^2}}{5+\frac{2}{x}-\frac{5}{x^2}}=[\frac{0+0}{5+0-0}]=\frac{0}{5}=0](/tpl/images/0237/6916/32e6e.png)
30.1
в)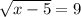
x-5=81
x=86
г)
7x-1=9
7x=10
x=10/7
30.2
в)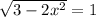
3-2x²=1
-2x²=-2
x²=1
x1=-1 x2=1
г)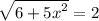
6+5x²=4
5x²=-2
x²=-0,4
x - не имеет решений
30.3
в)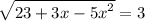
23+3x-5x²=9
5x²-3x-14=0
D=b²-4ac
D=9-4×5×(-14)=289
x1,2=-b+-*корень из дискриминанта*/2a
x1,2=(3+-17)/10
x1=-1,4
x2=2
г)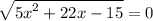
5x²+22x-15=0
D=484-4×5×(-15)=784
x1,2=(-22+-28)/10
x1=-5
x2=0,6