В каждом
примере необходимо
сделать преобразования -
раскрыть скобки,
умножить на число,
воспользоваться формулой
сокращенного умножения. В
результате получится квадратное
уравнение, необходимо
решить.
1. (x-2)(x-6)=5;
2. x 2 -2/3x=8/3;
3. (2x-5) 2 +24x=40.
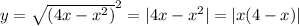
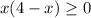 ,
, 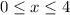
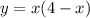 - парабола ветвями вниз
- парабола ветвями вниз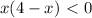 ,
,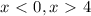
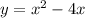 - парабола ветвями вверх
- парабола ветвями вверх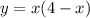 .
.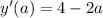
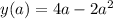
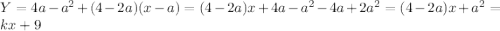
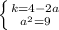
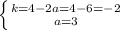
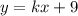 точки: (4;0), (2;4)
точки: (4;0), (2;4) - нет
- нет при k=-2.5 - да
при k=-2.5 - да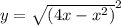 две общие точки.
две общие точки.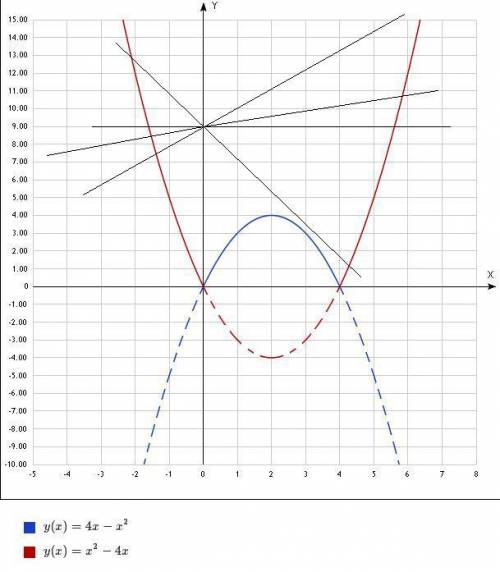
Периметр треугольника равен сумме трёх его сторон.
Одна сторона известна-это гипотенуза, равная 3√5 (см)
Найдем катеты, обозначив один катет за (х)см, тогда второй катет будет равным (х+3)см
Применим Теорему Пифагора:
с²=а²+в²
(3√5)²=х² +(х+3)²
9*5=х²+х²+6х+9
45=2х²+6х+9
2х²+6х+9-45=0
2х²+6х-36=0
х1.2=(-6+-D)2*2
D=√(36-4*2*-36)=√(36+288)=√324=18
х1,2=(-6+-18)/4
х1=(-6+18)/4=12/4=3
х2=(-6-18)/4=-24/4=-6- не соответствует условию задания
Отсюда:
первый катет, обозначенный за х=3 см, второй катет х+3=3+3=6см
Периметр прямоугольного треугольника равен:
3√5+3+6=(3√5+6) см
ответ: Катеты прямоугольного треугольника равны: 3см: 6см Р=(3√5+6)см