а)
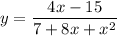
Знаменатель дроби не должен быть равен нулю. Получаем:
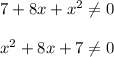
Чтобы это решить, для начала представим, что это выражение равно нулю, тогда получим квадратное уравнение и найдём его корни.
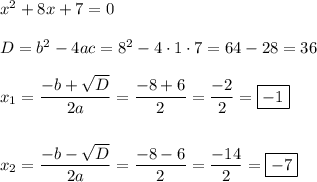
Но так как изначально это выражение было неравно нулю, то из области определения просто вычёркиваются корни уравнения, решённого нами выше.
ответ: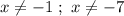 
.
б)
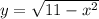
Подкоренное выражение всегда неотрицательно, то есть, больше или равно нулю.
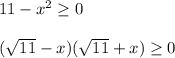
Решим неравенство методом интервалов.
Нули: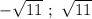 
- + -
---------------------
--------------------------
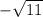
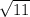
Нам нужно найти те промежутки, где выражение больше или равно нулю. Такой промежуток только один: ![[-\sqrt{11}\ ;\ \sqrt{11}]](/tpl/images/1574/8115/b27f8.png)
, так как там "+". Этот промежуток и будет являться областью определения функции.
ответ: ![x \in [-\sqrt{11}\ ;\ \sqrt{11}]](/tpl/images/1574/8115/4aef2.png)
.
Они равны
Объяснение:
Оба равны нулю