6x² - 11x - 2 < 0
Рассмотрим квадратичную функцию у = 6x² - 11x - 2. Графиком этой функции является парабола, ветви которой направлены вверх.
Выясним, как расположена эта парабола относительно оси Ох. Для этого решим уравнение 6x² - 11x - 2 = 0:
D = (-11)² - 4 · 6 · (-2) = 121 + 48 = 169; √169 = 13
х₁ = (11 + 13)/(2 · 6) = 24/12 = 2
х₂ = (11 - 13)/(2 · 6) = -2/12 = -1/6
Значит, парабола пересекает ось Ох в двух точках, абсциссы которых равны -1/6 и 2.
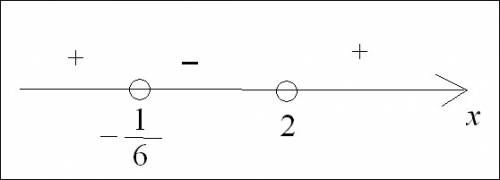
Покажем на чертеже, какие значения (по знаку) принимает функция на каждом из промежутков числовой оси (см. рис. в приложении).
х ∈ (-1/6; 2)ответ: (-1/6; 2).
ответ: 1
Объяснение:
Члены геометрической последовательности связаны следующим соотношением:
Нам даны три последовательных члена, для определённости дадим им номера 1, 2, 3.
Выпишем взаимосвязь 1-ого и 2-ого и 2-ого и 3-его:
Чтобы три числа были членами последовательности, должны выполнять оба равенства. Составим систему уравнений:
Поделим уравнения друг на друга (это действие можно выполнить, так как q ≠ 0, (7k + 1) ≠ 0, k + 15 ≠ 0):
Сокращаем на q ≠ 0 и перемножаем дроби "крест-накрест" (знаменатели в ноль не обращаются, учтено выше).
k₁ не является целым, поэтому не подходит. Остаётся один ответ k = 1.