арксинусом числа а из отрезка [-1;1] есть такой угол из [-π/2;π/2], синус которого равен а.
Одним словом, Ваши выражения не имеют смысла, если они не попадают в отрезок [-1;1]. Либо больше 1, либо меньше -1.
Из предложенных Вами это 2) arcsin 2, т.к. 2 больше1;
4) arcsin (-1.2), т.к. -1.2 меньше -1;
5) arcsin п/2, т.к. π≈3.14 и п/2 больше 1;
Дано:
<AOB и <COD
<COD внутри <AOB
AO ┴ OD; CO ┴ OB;
<AOB - <COD = 90°
Найти: <AOB и <COD.
Решение
Т.к . AO ┴ OD; CO ┴ OB,
то <AOD = 90; <COB = 90°.
<COD = <AOD - <AOC
<COD = <COB - <DOB
<COD = 90° - <AOC
<COD = 90° - <DOB
Получим
<AOC = 90° - <COD
<DOB = 90° - <COD
Следовательно <AOC = <DOB
2) По условию: <AOB - <COD = 90°
Но если от всего угла <AOB отнять <COD, то останутся два равных угла <AOC и <DOB, значит, это их сумма равна 90°.
<AOC + <DOB = 90° =>
<AOC = <DOB = 90°/2 = 45°
3) <COD = 90° - <DOB
<COD = 90° - 45°=45°
4) <AOB = <AOC + <DOB + <DOB
<AOB = 45° + 45° + 45° = 135°
ответ: <AOB - 135°; <COD =45°.

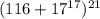
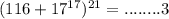
Не имеют смысла: arcsin2 (2>1) ; arcsin(-1,2) (-1,2<-1) ; arcsinП/2 (П/2>1) ;