ответ: 8.
Первый решение в лоб):
1·2·3·...·37 = 2³⁴·3¹⁷·5⁸·7⁵·11³·13²·17²·19·23·29·31·37 = 2²⁶·3¹⁷·7⁵·11³·13²·17²·19·23·29·31·37·10⁸
На 8 нулей оканчивается т.к. 10⁸. И другие множители не дадут нулей в конце.
Покажу, как разложить на простые множители такое произведение, на примере множителя 2.
От 1 до 37:
36:2=18 чисел кратных 2.
36:4=9 чисел кратных 4.
32:8=4 числа кратных 8.
32:16=2 числа кратных 16.
32:32=1 число кратное 32.
С каждой следующей кратность мы подсчитываем по одной 2 в множителя чисел. Поэтому всего 2 встречается 18+9+4+2+1=34 раза.
Второй проще предыдущего):
Количество нулей числа зависит от того, сколько раз встречается 5 и 2 при разложении этого числа на простые множители т.к. 10=2·5.
Как и в первом подсчитаем, что всего 34 двойки и 8 пятёрок. Значит, можно "составить" не более 8 десяток. И будет 8 нулей в конце.
8
Объяснение:
В конце произведения получим 0, если 5 умножается на чётное число. То есть количество нулей в конце N! зависит от количества 2 и 5 в произведении. Так как в произведении 1•2•3•4•...•37 количество 2 больше чем 5, то достаточно посчитать количество 5:
5, 10=2·5, 15=3·5, 20=4·5, 25=5·5, 30=6·5, 35=7·5 - количество 5 равен 8.
Значит, произведение 1•2•3•4•...•37 оканчивается на 8 нулей.
Количество нулей в конце N! определяется по формуле
![\tt \displaystyle S(N)=\left [\frac{N}{5} \right]+\left [\frac{N}{25} \right]+\left [\frac{N}{125} \right]+...,](/tpl/images/0612/8543/b9dbf.png)
где [a] - целая часть числа a.
Так как 1•2•3•4•...•37=37! и
![\tt \displaystyle \left [\frac{37}{5} \right]=7, \;\left [\frac{37}{25} \right]=1, \; \left [\frac{37}{125} \right]=0,](/tpl/images/0612/8543/77070.png)
то
S(37)=7+1=8.
Тип: дифференциальное уравнение второго порядка, допускающее понижения порядка.
Пусть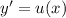 , тогда
, тогда 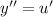 , получаем :
, получаем :
Умножим обе части уравнения на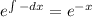 , получаем
, получаем
Интегрируем обе части уравнения
В правой части уравнения интеграл будем считать путём интегрирования по частям
Выполним обратную замену
ответ: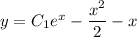 .
.