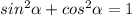Объяснение:
свойство пропорции
Чтоб найти косинус используем формулу основного тригонометрическо тождества:
Объяснение:
Чтоб найти косинус используем формулу основного тригонометрическо тождества: