ответ: 24 км/ч.
Объяснение: Пусть х км/ч скорость лодки в стоячей воде, тогда скорость лодки по течению реки х+3 км/ч, а против течения х-3 км/ч. Времени по течению реки, на расстояние в 9 км, лодка затратила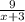 
часов и против течения реки, на расстояние в 14 км, лодки затратила 
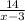часов, что в сумме будет равно времени затраченным на расстояние в 24 км, в стоячей воде, это 
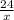часов. Составим уравнение:
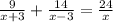
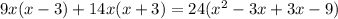
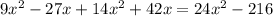
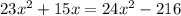
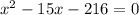
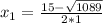
x₁=(-9) км/ч не подходит, т.к. скорость не может быть отрицательной.
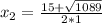
x₂=24 (км/ч) скорость лодки в стоячей воде.
ответ: 24 км/ч.
Объяснение: Пусть х км/ч скорость лодки в стоячей воде, тогда скорость лодки по течению реки х+3 км/ч, а против течения х-3 км/ч. Времени по течению реки, на расстояние в 9 км, лодка затратила 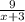часов и против течения реки, на расстояние в 14 км, лодки затратила 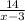часов, что в сумме будет равно времени затраченным на расстояние в 24 км, в стоячей воде, это 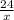часов. Составим уравнение:
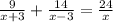
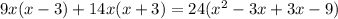
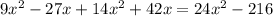
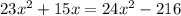
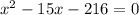
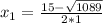
x₁=(-9) км/ч не подходит, т.к. скорость не может быть отрицательной.
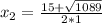
x₂=24 (км/ч) скорость лодки в стоячей воде.
ответ: { 1/3 }.
Объяснение:
9х²+1≤6х;
9х²-6х+1≤0;
(3х-1)²≤0;
f(х)=(3х-1)²; f(х)=0 при х=1/3;
По методу интервалов:
при х∈(-∞;1/3] f(х)≥0 ;
при х∈[1/3;+∞) f(х)≥0 ;
значит f(х)≤0 при х∈{ 1/3 }.