1) 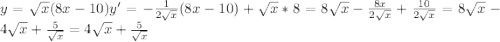
2) 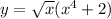
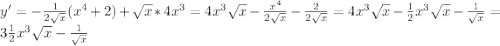
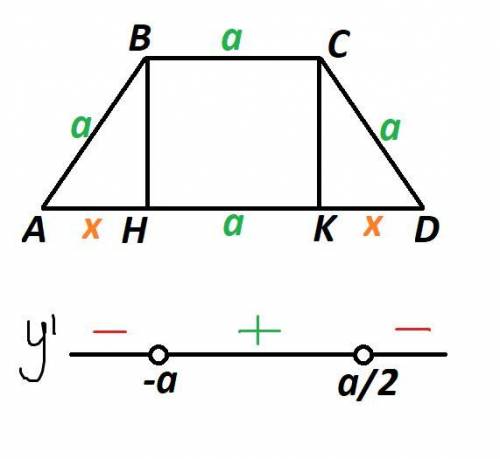
Рассмотрим трапецию ABCD.
Основания трапеции не могут иметь одинаковую длину, так как в противном случае это будет параллелограмм. Значит, одно из оснований BC и две боковые стороны AB и CD равны по а. Заметим, что рассматриваемая трапеция равнобедренная.
Проведем высоты BH и CK. Тогда, HK=а.
Обозначим AH=KD=х.
Высоту трапеции найдем по теореме Пифагора:
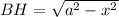
Запишем выражение для площади трапеции:
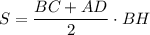
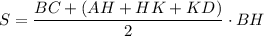
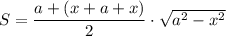
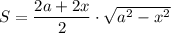
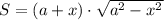
Исследуем на экстремумы функцию S. Найдем производную:
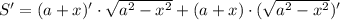
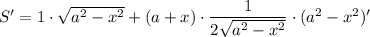
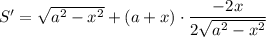
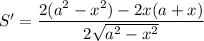
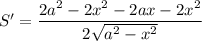
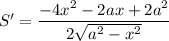
Найдем нули производной:
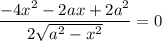
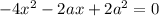
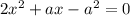
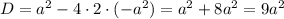
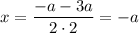
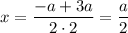
При переходе через точку 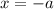 производная меняет знак с минуса на плюс, значит это точка минимума.
производная меняет знак с минуса на плюс, значит это точка минимума.
При переходе через точку 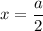 производная меняет знак с плюса на минус, значит это точка максимума.
производная меняет знак с плюса на минус, значит это точка максимума.
Таким образом, наибольшую площадь трапеция имеет при 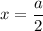 . Эта площадь равна:
. Эта площадь равна:
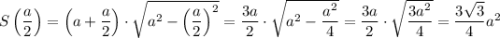
ответ: 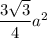
1) произв у=1/2√х*(8х-10)+√х*8
2) произв у=1/2√х*(х⁴+2)+√х*4х³