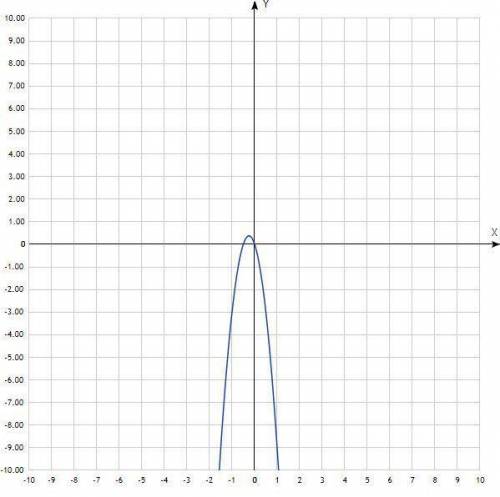
График в файле.
Объяснение:
y=-6x²-3x
функция квадратичная вида ax²+bx+c - значит парабола
аргумент а - отрицательный, значит ветви параболы направлены вниз.
с=0, значит одна из ветвей пересекает ось Оу в точке с координатой у=0, если так, то и ось Ох она пересекает с координатой х=0, т.е. ветвь параболы проходит через начало координат.
находим точки пересечения с осью Ох
-6х²-3х=0
-3х(2х+1)=0
х1=0
2х+1=0
2х=-1
х2=-1/2
находим вершину параболы
х=-b/(2a)
x=3/-12=-1/4
y=-6*(-1/4)²-3*(-1/4)=3/8
(-1/4;3/8) - координаты вершины
Строим график.
Объяснение:
1) (a-5)(a+3) < (a+1)(a-7)
a^2-5a+3a-15 < a^2+a-7a-7
-2a-15 < - 6a-7
4a < 8
a < 2
Это неравенство верно вовсе не при любых а, а только при а меньше 2.
2) [5x+2] <= 3
Видимо, квадратные скобки это модуль. Неравенство распадается на два:
а) 5x+2 >= - 3
5x >= - 5
x >= - 1
б) 5x+2 <= 3
5x <= 1
x <= 1/5
Целые решения: - 1; 0
3) Пусть одна сторона равна 5 см, а другая больше неё в 4 раза, то есть 20 см.
Тогда периметр равен 2*(5+20) = 2*25 = 50 см.
Если первая сторона меньше 5 см, то вторая меньше 20 см, а периметр меньше 50 см.