Решите уравнение
ОДЗ уравнения: все числа.
Преобразуем уравнение, воспользуемся формулой двойного аргумента cos2x = 2cos2x – 1, получим:
2cos2x – 1 – cosx = 0
2cos2x – cosx – 1 = 0
Введем новую переменную, пусть cosx = a, тогда
2a2 – a – 1 = 0
D = 9
a1 = 1 и a2 = — 1/2
Вернемся к первоначальной переменной, получим 2 уравнения:
cosx = 1 и cosx = — 1/2
Решим 1 уравнение:
cosx = 1
Задание13в21_1
Решим 2 уравнение:
cosx = — 1/2
Задание13в21_2
Задание13в21_3
Все три корня можно объединить в один, для этого воспользуемся единичной окружностью
Задание13в21_4
Из рисунка видно, что корни повторяются через 2π/3, тогда
Задание13в21_5
В решении.
Объяснение:
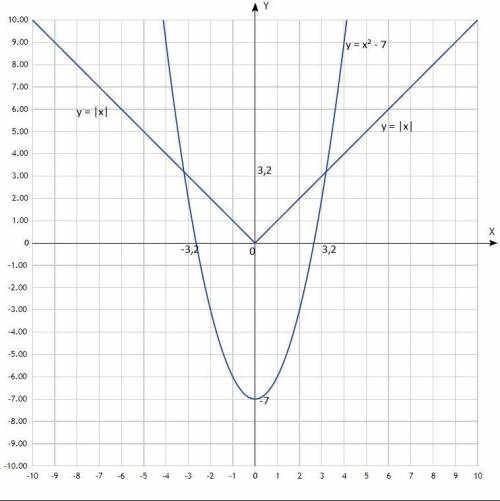
Решить графически систему уравнений:
у = х² - 7
у = |x|
Первый график - парабола со смещённым центром, ветви направлены вверх.
Второй график - график функции модуля (значения у всегда > 0).
Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.
у = х² - 7 у = |x|
Таблицы:
х -4 -3 -2 -1 0 1 2 3 4 х -3 -2 -1 0 1 2 3
у 9 2 -3 -6 -7 -6 -3 2 9 у 3 2 1 0 1 2 3
По вычисленным точкам построить графики.
Согласно графиков, координаты точек пересечения:
(-3,2; 3,2); (3,2; 3,2).
Решения системы уравнений: (-3,2; 3,2); (3,2; 3,2).
Объяснение:
Первая функция:
y: 3.0625 |3.25 | 4| 7
x: -1| 0 | 1 | 2
Расставляем точки с данными координатами, соединяем их линией и получаем график функции
Вторая функция:
Для начала запишем ОДЗ: 2x-4>0=> 2x>4=> x>2
Начинаем записывать x от 3
y: 1| 2 | 12
x: 3| 4| 6|
Опять же ставим точки с заданными координатами и соединяем их линией