5% = 0,05; 4% = 0,04
Пусть вкладчик внёс на первый счёт х грн, тогда доход по этому счёту составил 0,05х грн.
Пусть вкладчик внёс на второй счёт у грн, тогда доход по этому счёту составил 0,04у грн.
Если средства, внесённые на разные счета, поменять местами, то годовой доход по двум вкладам составит
0,04x + 0,05y = A гривен.
Составим систему
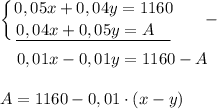
1) Если средства, внесённые на два счёта были одинаковы, то годовой доход не изменится :
x = y, x - y = 0, A = 1160
2) Если на первый счёт было внесено больше денег, чем на второй счёт, то годовой доход уменьшится :
x > y, x - y > 0, A < 1160
3) Если на первый счёт было внесено меньше денег, чем на второй счёт, то годовой доход увеличится :
x < y, x - y < 0, A > 1160
ответ : изменение годового дохода будет зависеть от количества внесённых денежных средств на разные счета.
х² - 2х + 1 - х² + 4 = х - 4
-2х -х = -4 - 4 - 1
-3х = -9
х = -9 / -3 = 3.
2) 5/x-x/3=0,2 0,2 = 2/10 = 1/5
Приводим к общему знаменателю 15х:
5*15-х*5х=3х
Получаем квадратное уравнение: 5х² + 3х - 75 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=3^2-4*5*(-75)=9-4*5*(-75)=9-20*(-75)=9-(-20*75)=9-(-1500)=9+1500=1509;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√1509-3)/(2*5)=(√1509-3)/10=√1509/10-3/10=√1509/10-0.3≈3.58458491991101;
x_2=(-√1509-3)/(2*5)=(-√1509-3)/10=-√1509/10-3/10=-√1509/10-0.3≈-4.18458491991101.
3) (X - 5)^2=(5 - x)^2
x² - 10x + 25 = 25 - 10x + x² - это тождество при любом х.
4) (X-2)^2-(x-1)*(x+)=x-5 - тут пропущена цифра.
5) X/7x/5=0,2 - тут знак пропущен
6) (X-2)^2=(3-x)^2
х² - 4х + 4 = 9 - 6х + х²
-4х + 6х = 9 - 4
2х = 5
х = 5 / 2 = 2,5.