а = 3, в = 4, с = 5. Треугольник прямоугольный, т.к 5² =3² + 4²
Биссектриса внутреннего угла тр-ка делит противолежащую углу сторону на части, пропорциональные прилегающим сторонам, т.е гипотенуза с поделена на отрезки: х, прилегающий к стороне а и (с-х), прилегающий к стороне b.
а:a1 = b:b1
3:х = 4:(5-x)
15 - 3x = 4x
7x = 15
a1 = x = 15/7
b1 = 5-x = 5 - 15/7 = 20/7
Сама биссектриса равна:
Lc = √(a·b - a1·b1)
Lc = √(3·4 - 15/7· 20/7)= √(12 - 300/49) = √(588/49 - 300/49) = √(288/49) =
12√2/7
ответ: 12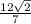
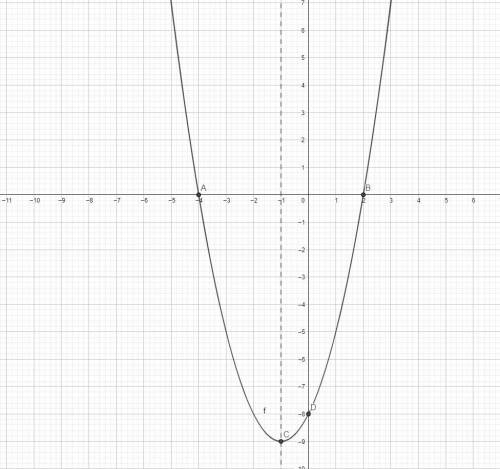
y = x² + 2x - 8
y = x² + 2x + 1 - 9 = (x + 1)² - 9
Видим, что график смещён вниз на 9 единиц и влево на 1 единицу. Соответственно, вершина данного графика будет с координатами: (-1; -9).
Найдём точки пересечения с осью OX, решив уравнение: x² + 2x - 8 = 0.
По т-ме Виета корни: -4; 2. То есть, график пересекает ось ОХ в точках (-4; 0) и (2; 0).
График также проходит через точку (0; -8) - это характерная точка (то есть, если подставить 0 вместо х, мы получим лишь свободный член, это -8).
Ось симметрии: x = -1.
Строим график по полученным точкам.
Объяснение:
16-9b²=(4-3b)(4+3b)