ответ:1)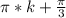
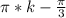
2) НЕТ ДЕЙСТВИТЕЛЬНЫХ РЕШЕНИЙ
Второе даже решать не буду там и так ясно что нет решений а первое вот:
1)разложи косинус получишь
4 sin^4 x = 5-5*sin^2(x) + 1
2)заменяем sin^2 x=t
-1<t<1
4*t^2=5-5*t+1
4*t^2+5t-6=0
t=-2 t=3/4 (по т.виета)
||
\/
sin^2 x=-2 sin^2 x = 3/4
нет решений
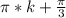
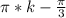
т.к. sinx=корень из 3/ 2
тк -1<sinx<1 x=arcsin( корень из 3/ 2)+pi*k
x=-arcsin( корень из 3/ 2)+pi*k
arcsin( корень из 3/ 2)=pi/3
отсуда
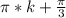
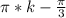
4х-у=17
6х+у сложения, получаем:
10х=40
х=4
Следовательно -у=1; у=-1.
ответ: 4;-1.
6х-10у=11
5у+7х вычитания, получаем:
-х-15у=-8
х+15у=8 (поменяли знак выражения)
х=8-15у (выражаем одну переменную через другую, далее подставляем в выражение)
6(8-15у)-10у=11
48-90у-10у=11
-100у=-37
у=0,37
Следовательно, х=8-15*0,37, что составит 2,45.
ответ: 2,45;0,37
2х-у/3 - х-2у/2 = 3/2
2х+у/2 - х+2у/3 = 1/3
Домножаем на 6 - общий знаменатель, получаем:
4х-2у-3х+6у=9
6х+3у-2х-4у=2
х+4у=9
4х-у=2
х=9-4у (выражаем одну переменную через другую и подставляем значение в выражение)
4(9-4у)-у=2
36-16у-у=2
-17у=-34
у=2
Следовательно х=9-4*2, что составит 1.
ответ: 1;2
1-sin4a = 2sin²(45°-2a)
Применяем основное тригонометрическое тождество:
1 = cos²x+sin²x, только вместо х берём аргумент (45°-2а), получаем:
cos²(45°-2a)+sin²(45°-2a) -sin4a -2sin²(45°-2a) = 0
Приводим подобные слагаемые, упрощаем выражение, получаем:
cos²(45°-2a)-sin²(45°-2a) -sin4a = 0
Применяем формулу косинуса двойного угла cos²x-sin²x=cos2x
cos[2(45°-2a)] - sin4a = 0
cos(90°-4a) - sin4a = 0
Применяем формулу приведения: cos(90°-x) = sinx
cos4a - cos4a = 0
0 = 0
Тождество доказано