Дайте решение ВАРИАНТ – 2.
Задания с выбором ответа. (рейтинг задания 0, )
При выполнении заданий А1-А5, обведите цифру, соответствующую правильному ответу.
А-1. Решите неравенство -2х < 4
1. ( - ∞; 2] 2. (-2 ; ∞) 3. [ -2; ∞) 4. ( - 2; 4]
А-2. Определите число целых решений неравенства -1 ≤ х ≤ о
1. семь 2. три 3. четыре 4. два
А-3. Какой промежуток включает в себя все решения неравенства 2 < х ≤ 4
1. [ 3; 4] 2. [ -2; 5) 3. ( -3; 2) 4. ( - ∞; 2] U [2; 4)
А-4. Найдите число целых отрицательных решений неравенства х ≥ - 3
1. три 2. ни одного 3. четыре 4. бесконечно много
А-5. Найдите сумму целых чисел неравенства х ≤ 6 , лежащих на промежутке [0; 2]
1. 3 2. 6 3. 7 4. 2
Задания с кратким ответом. (рейтинг задания 0, )
При выполнении заданий В1-В5, запишите полученный ответ в виде промежутка или цифры.
В-1. Решите неравенство 3(3х – 1) > 2х + 4
В-2. Найдите наименьшее целое число, удовлетворяющее неравенству 3 –3 ( х – 5) < 0
В-3. При каких значениях n выражение 2n-7 больше или равно 5 ?
Задания с развернутым ответом. (рейтинг задания )
При выполнении заданий С1 – С2 запишите сначала номер выполняемого задания, а затем полное решение с необходимым обоснованием полученного ответа.
С-1. При каких значениях переменной выражение √2х + 8 имеет смысл?
С-2. Длина стороны прямоугольника 4см. Какой должна быть длина другой стороны, чтобы периметр прямоугольника был больше периметра квадрата со стороной 3см?
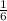( т.к. надо разделить благоприятные исходы на кол-во всех событий. 2) Всего событий- 6 ( по той же причине , что и в первой) Благоприятных исходов- 3 (т.к. менее 4 очков должно выпасть, а это, либо 1 либо 2 либо 3) Р(В)=
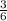, а это равно 
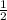( или по другому 0,5)
Тогда имеем:
13A1+78d=130(из формулы суммы первых членов арифметической прогрессии Sn=((2A1+d(n-1))/2)*n), что равносильно
A1+6d=10
A4=A1+3d=B1
A10=A1+9d=B1*q
A7=A1+6d=B1*q^2
B1*q^2=10
B1+3d=10
B1+6d=B1*q
B1=10/q^2(Выражаем B1 из первого уравнения)
B1=10-3d(Выражаем B1 из второго уравнения)
3d=10-B1(теперь 3d из второго)
3d=10-10/q^2(подставляем сюда значение B1 из первого)
10+3d=10/q(подставляем вместо B1 соответственно 10-3d и 10/q^2)
10+10-10/q^2=10/q
20-10/q^2-10/q=0
20q^2-10q-10=0
2q^2-q-1=0
D=1+8=9
q1=(1-3)/4=-1/2
q2=(1+3)/4=1
Зная q, можно найти все остальное:
B1*q^2=10
B1=10/q^2
3d=10-B1
Для q=-1/2 B1=40, 3d=10-40=-30, d=-10
Для q=1 B1=10, 3d=10-B1=0, d=0.
Так как нам известно что первый член арифметической прогрессии не равен второму, то корень q=1 не подходит (так как d=0). Значит, d=-10.
Найдем A1.
A1+3d=B1
A1-30=40
A1=70.
ответ: A1=70.