1.
Укажите выражение, которое является квадратом разности одночленов (-5у) и 3х
-25у2 - 9х2
25у2 - 9х2
(-5у - 3х)2
-(5у + 3х)2
2.
Укажите выражение, которое является квадратом суммы одночленов 7х и (-2у)
(7х + 2у)2
49х2 + 4у2
49х2 - 4у2
(7х - 2у)2
3.
Раскройте скобки (3а - 5в)2
9а2 -15ав - 25в2
9а2 - 30ав + 25в2
9а2 + 25в2
9а2 - 25в2
4.
Раскройте скобки (7в + 2а)2
49в2 + 14ав + 4а2
49в2 + 4а2
49в2 + 28ав + 4а2
49в2 + 28а2в2 + 4а2
5.
Раскройте скобки (-3в + 6а)2
36а2 - 36ав - 9в2
36а2 - 9в2
-36а2 + 9в2
36а2 - 36ав + 9в2
6.
Раскройте скобки (-5а - 4в)2
-(25а2 + 40ав + 16в2)
25а2 + 40ав + 16в2
25а2 - 40ав - 16в2
-25а2 - 16в2
7.
Разложите на множители 9х6 - 54х3у5 + 81у10
(3х3 - 9у5)(3х3 + 9у5)
(9х3 - у5)(х3 + 81у5)
(3х3 - 9у5)2
(3х3 + 9у5)(3х2 - 9у2)
8.
На какой одночлен нужно заменить звездочку (*), чтобы равенство (х + (*))2 = х2 -10ху + 25у2
такого одночлена не существует
5у
-5у
-10у
9.
Известно, что х + у = -4, а ху = -32. Вычислите значение выражения х2 + у2
(Подсказка: воспользуйтесь формулой квадрата суммы - найдите квадрат суммы х + у, выполните необходимую замену).
ответ: .
10.
Вычислите, используя формулу квадрата суммы, 612
(Подсказка: запишите число 61 в виде суммы).
ответ:.
1) проверяем условие при наименьшем возможном значении n.
n>5, значит проверяем условие при n=6
Верно!
2) Сделаем предположение, что для всех n=k, k>5 верно неравенство:
3) Тогда при n=k+1 должно выполняться неравенство:
Вернемся к неравенству из второго пункта и домножим его на 2:
Подставим 2k² в 3-й пункт и рассмотрим полученное неравенство:
по методу интервалов определяем, что неравенство k²-2k-1>0 выполняется при k>1+√2, тогда при k>5 оно тоже выполняется (так как 5>1+√2)
Тогда обратным ходом получаем 2k²>k²+2k+1 при k>5 или 2k²>(k+1)² при k>5
Если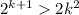
, а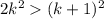 
, при k>5
То есть,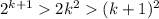
, при k>5, то по закону транзитивности: