Объяснение:
почему вопрос только к "иксу в кубе"?
почему не возникает вопрос к " (х-1) в четвертой?
МЕТОД ИНТЕРВАЛОВ:
1. найти корень каждого множителя:
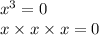
х1=0, х2=0, х3=0
нечётное количество одинаковых корней, => знаки при переходе через точку х=0 меняем.
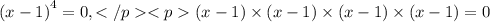
х1=1, х2=1, х3=1, х4=1
четное количество одинаковых корней, => знаки при переходе через точку х=1 не меняем
х+5=0, х=-5
1-4х=0, х=0,25
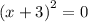
х1=-3, х2=-3
.... знаки не меняем
х-8=0, х=8
2. на числовой прямой в порядке возрастания расположить корни множителей, определить знак выражения на каждом промежутке
продолжение на фото
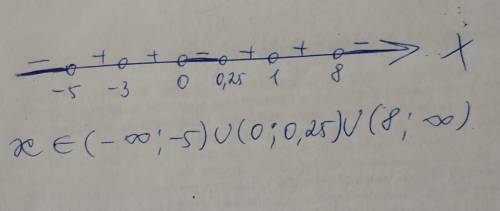
1) x²-8x+20=0
D=(-8)²-4*20=16-80=-64<0 ⇒ нет действительных корней ⇒ нельзя разложить на множители квадр. трёхчлен
2)х²-1=(х-1)(х+1)
3)х²-8х+15=(х-3)(х-5) , так как
D=(-8)²-4*15=64-60=4>0 ⇒ есть два действ. корня
х₁=(8-2)/2=3 , х₂=(8+2)/2=5
4)х²-9х+20=(х-4)(х-5) , так как
D=(-9)²-4*20=81-80=1>0 ⇒ есть два действ. корня
х₁=4 , х₂=5
Примечание: если D=0, то есть два равных корня х₁=х₂
если D<0, то нет действ. корней, а есть комплексные корни
3х^2- 18x = 0
3x(x-6)=0
3x=0 x-6=0
x=0 x=6