|x| - это расстояние от нуля до x, поэтому решением этой системы неравенств (ведь тут не одно неравенство, а два) является объединение двух интервалов (-10; -4)∪(4;10). Концы интервалов в ответ не входят, поэтому подсчитываем количество целых решений внутри; достаточно подсчитать их количество в одном из них и удвоить: 5·2=10
ответ: 10
Замечание 1. Если бы интервал был бы большим, мы бы придумали, как подсчитать количество целых точек на основании концевых точек, но здесь легче их просто пересчитать.
Замечание 2. И все-таки хочется придумать общую формулу. Если интервал (m;n), где m и n - целые числа и m<n, то целых чисел внутри n-m-1.
x³=t
t²-5t+4=0
t₁+t₂=5 (-за теормою Виета)
t₁*t₂=4
t₁=4
t₂=1
х³=t
x=∛t
x₁=∛4
x₁≈1.5874
x₂=∛1
x₂=1
x=∛4 и х=1
2*х²- х -3≥ 0
__+____-1____-___1.5____+______>x
x∈(-∞; -1]∪[1.5; +∞)
y=cosx-1
а) Область определения: D (cos x-1) = R .
б) Множество значений: E (cos x-1 ) = [ – 2 , 0]
в) Четность, нечетность: функция четная.
г) Периодичность: функция периодическая с основным периодом T = 2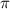
Точки пересечения с осямии:ОХ:
cos x -1= 0
cos x =1
OY:
cos(0)-1=1-1=0
Промежутки знакопостоянства.:
cosx-1>0
сosx>1 - не существует, поэтому функция лежит ниже оси ОХ
интервалы возрастания и убывания:
y'=(cosx-1)'= (cosx)'-1'= -sinx
функция возрастает:
-sinx>0
функция убывает:
-sinx<0
Экстремумы:
(-sinx)'= -cosx
-cos(0)=-1
-1<0 значит точка x = 0 точка максимума функции