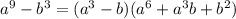По оси х: 9 и (-9)
По оси у: 9 и (-9)
Объяснение:
Общий вид уравнения окружности:
(x-x0)^2 + (y-y0)^2 = R^2
Где (х0, у0) координаты центра окружности, а R - ее радиус
Если окружность имеет центр в начале координат, то уравнение примет вид:
х^2 + у^2 = R^2
Последнее уравнение похоже на данное нам, поэтому делаем вывод, что окружность имеет центр в начале координат, а ее радиус равен корню из 81. Т.е. радиус равен 9. На основе выше сказанного можно утверждать, что окружность пересекает оси координат в точках:
По оси х: 9 и (-9)
По оси у: 9 и (-9)
№1
a) (2x - 1)² = 4x² - 4x + 1
б) (3a + c)² = 9a² + 6ac + c²
в) (y-5)(y+5) = y² - 25
г) (4b + 5c)(4b - 5c) = 16b² - 25c²
№2
(x + y)(x - y) - (x² + 3y²) =
x² -y² -x² - 3y² =
-y² - 3y² =
-4y²
№3
а) 16y² - 0,25 = 0,25 (64y² - 1) = 0,25 (8y - 1)(8y + 1)
б) a² + 10ab +25b² = (a + 5b)²
№4
(5 - x)² - x(2,5 + x) = 0
25 - 10x + x² - 2,5x +x² = 0
25 - 12,5x = 0
-12,5x = -25
x = 2
№5
a) (2a - b²)(2a + b²) = 4a² -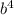
б) (x-6x³)² = 36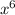
- 12
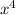+ x²
в) (y + b)²(y - b)² = ((y + b)(y - b))² = (y² - b²)² =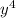
- 2b²a² +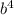
№6
а)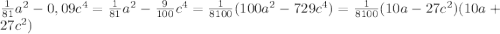
б)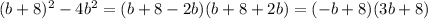
в)