Производная функции у = х²/2 равна (1/2)*2х = х.
Уравнение касательной: у(кас) = y'(xo)*(x - xo) + y(xo).
Так как касательная проходит через точку М((1/2)4 -1), то подставим её координаты в уравнение.
-1 = xo((1/2) - xo) + (xo²/2).
-1 = (xo - 2xo² + xo²)/2.
Получаем квадратное уравнение:
хо² - хo - 2 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:
D=(-1)^2-4*1*(-2)=1-4*(-2)=1-(-4*2)=1-(-8)=1+8=9;
Дискриминант больше 0, уравнение имеет 2 корня:
xo_1=(√9-(-1))/(2*1)=(3-(-1))/2=(3+1)/2=4/2=2;
xo_2=(-√9-(-1))/(2*1)=(-3-(-1))/2=(-3+1)/2=-2/2=-1.
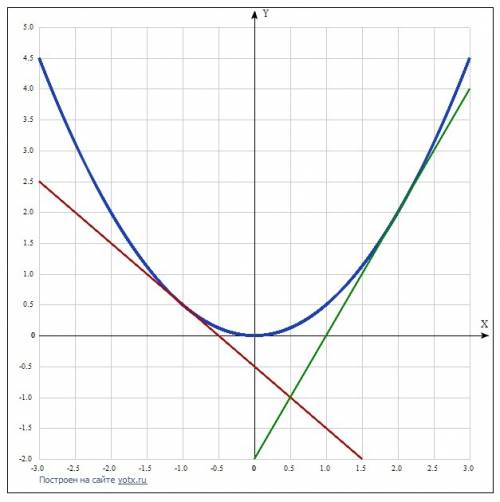
Получили 2 точки касания хo = -1 и хo = 2.
Определяем уравнения касательных.
ук1 = -1(х + 1) + (1/2) = -х - (1/2).
ук2 = 2(х - 2) + 2 = 2х - 2.
Находим координаты точки их пересечения:
-х - (1/2) = 2х - 2,
3х = 1,5 = 3/2,
х = 1/2, у = -(1/2) - (1/2) = -1. Точка ((1/2); -1).
Находим координаты точек пересечения касательных с осями координат: с осью Ох пересекается:
- кас(1), при этом у = 0: -х - (1/2) = 0. х = -(1/2),
- кас(2), при этом у = 0: 2х - 2 = 0. х = 1.
С осью Оу пересекается:
- кас(1), при этом х = 0: у = -2.
Полученный четырёхугольник разобьём на 2 фигуры: прямоугольная трапеция и прямоугольный треугольник. Их площади равны соответственно S1 и S2.
S1 =(((1/2) + 1)/2)*(1/2) = 3/8.
S2 = (1/2)*1*(1/2) = 1/4 = 2/8.
Тогда искомая площадь S = S1 + S2 = (3/8) + (2/8) = 5/8.
Заметим, что при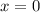
левая и правая часть уравнения обращается в 0. Значит, число 0 является корнем этого уравнения.
Предположим, что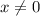
. Тогда, мы можем разделить обе части равенства на 
. Получим:
Рассмотрим левую часть.
Вспомним, что функция вида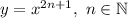
является возрастающей на всей области определения, то есть на множестве действительных чисел. Тогда и функция 
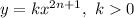является возрастающей. Сумма возрастающих функций также является возрастающей.
Применительно к данному уравнению можно записать: функции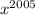
, 
, ..., 
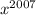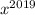возрастают, тогда и функции 
, 
, ..., 
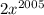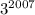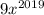также возрастают, а значит возрастает и их сумма.
Таким образом, функция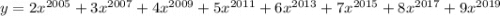
возрастает. Это означает, что каждое свое значение она принимает только в одной точке.
Следовательно, уравнение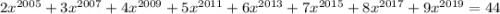
может иметь не более одного решения.
Решение уравнения легко подбирается: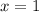
. Действительно, сумма коэффициентов в левой части уравнения равна 44:
В силу сказанного выше, других корней у уравнения нет.
ответ: 0; 1