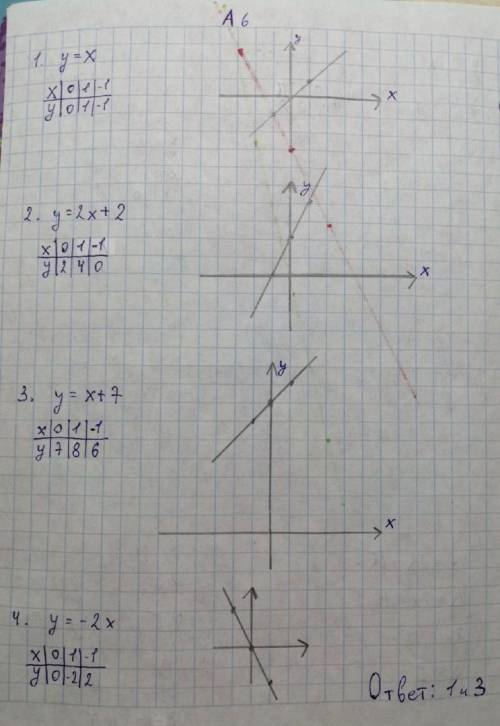
А6 - 1,3
В1 - (20;20)
В2 - (2;0)
С1 - 2
С2 - (фотка)
Объяснение:
А6. решение на фото
В1. чтобы найти координату пересечения графиков функции нужно их прировнять
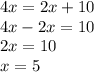
Найдём Y если подставим полученное значение Х в функцию (можно подставить в любую)
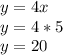
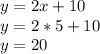
Точка пересечения графиков функции имеет следующие координаты (20;20)
В.2
Ось абсцисс - это ось ОХ
Чтобы найти координату пересечение графика функции с осью абсцисс
Нужно прировнять Y к 0, так как нам нужно пересечение графика функции с осью абсцисс
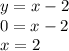
Точка пересечение графика функции с осью абсцисс имеет следующие координаты (2;0)
С.1
Мы имеем функцию 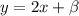 и точку с координатами (0;2)
и точку с координатами (0;2)
Чтобы найти b мы подставим координаты точки в функцию
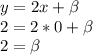
С.2 решение на фото
( 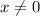 так как при делении любого выражения на 0 получается неопределённое выражение)
так как при делении любого выражения на 0 получается неопределённое выражение)
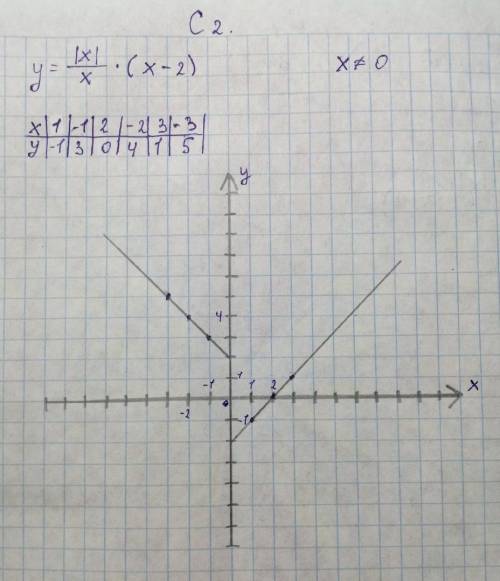
5х + 17у = 20, если у = 0
5х + 17 · 0 = 20
5х = 20
х = 20 : 5
х = 4
ответ: (4; 0).