1.В треугольнике АВС А(3;-1;1), В(-5;3;1), С(1;5;3). Найти координаты точки М, если:
• 1 вариант АМ1 – медиана. М1 (-2;4;2)
• 2 вариант ВМ2 – медиана. М2 (2;-2;2)
• 3 вариант СМ3 – медиана. М3 (-1;1;1)
2.Определите координаты центра окружности, диаметром которой является отрезок АВ, если А (4; – 2; 12), В (1; 3; -8).
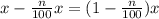рублей.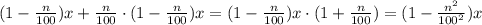
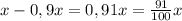
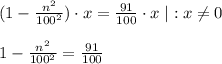
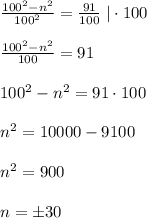
ВСМ=80
2)а) не знаю
б) рассмотрим АВК ВК=12 АК=4
По т.Пифагора
АВ=\/144+16=4\/40 (\/-это квадратный корень)
S abk=1/2*4*12=24
S abcd=24*2+12*5=108
3)Предположим, что это так, значит тр. ВОС и тр. AOD подобны,значит ВО/ОD=СО/ОА, 6/12=5/15, 3=3, значит треугольники действительно подобны (по двум сторонам и углу между ними), значит 3*SВОС=SАОD из следствия подобия треугольников угол ВСО = углу ОАD, углы являются накрест лежащими при прямых ВC и AD, значит ВС// AD, следовательно по признаку AВCD- трапеция.
Т.к отношение площадей треугольников равно квадрату коэффициента подобия, то к=3,а SАОD /SВОС=3^2, т.е 9.