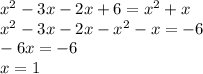
х∈(-∞, -6), решение системы неравенств.
Объяснение:
Решить систему неравенств:
−x+4>0
5x<−30
Решим первое неравенство:
−x+4>0
-x> -4
x<4 знак меняется
х∈(-∞, 4)
Решения неравенства в интервале от -бесконечности до 4.
Неравенство строгое, скобки круглые.
Решим второе неравенство:
5x<−30
х< -6
х∈(-∞, -6)
Решения неравенства в интервале от -бесконечности до -6.
Неравенство строгое, скобки круглые.
Теперь нужно на числовой оси отметить оба интервала и найти пересечение решений, то есть, такое решение, которое подходит двум данным неравенствам.
Пересечение х∈(-∞, -6), это и есть решение системы неравенств.
Потрібно знайти суму чисел: 10 + 15 + 20 + ... + 95.
Цей ряд чисел утворює арифметичну прогресію, тобто послідовність чисел, кожен член якої, починаючи з 2-го, дорівнює попередньому, складеному з одним і тим же числом, званим різницею прогресії - це число 5.
Маємо: а₁ = 10, різниця d = 5.
Знайдемо номер останнього члена прогресії, рівного 95:
an = a₁₁ + d (n - 1) - формула n-го члена
95 = 10 + 5 (n - 1),
10 + 5n - 5 = 95,
5 + 5n = 95,
5n = 95 - 5,
5n = 90,
n = 90: 5,
n = 18.
Значить, все двозначних чисел, кратних числу 5, - 18 штук.
Знайдемо S₁₈.
Sn = (a₁ + a₁₈) / 2 · n - формула суми n перших членів арифметичної прогресії
S₁₈ = (10 + 95) / 2 · 18 = 105 · 9 = 945.
Відповідь: 945.
Объяснение:
х=1