Объяснение:
1) А(-π/2 ; -1).
Здесь х= - π/2;
Для определения принадлежит ли точка А графику функции y=cos x
подставим значение х= - π/2, в формулу данной ф-ции:
y=cos x = cos (-π/2) =0. Итак при х= -π/2 , значение ф-ции у=0, а
это значит что точка А(-π/2;-1) не принадлежит графику функции
y=cos x.
2) B(9π/4; √2/2).
Объяснение аналогично варианту 1).
x= 9π/4;
Подставляем значения х в формулу данной функции:
y=cos x= cos(9π/4) = cos(2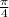
) =cos(π/4 + 2π)= cos(π/4)= √2/2;
При х =9π/4, значение функции у=√2/2, то точка В(9π/4; √2/2)
принадлежит графику функции y=cos x.
3) C(-4π;-1).
x=-4π; y=cos x= cos(-4π)=cos(-2π-2π)=cos(-2π)=cos(2π)=1;
При х= -4π, у=1.
Точка В(-4π;-1) не принадлежит графику функции y=cos x.
2) ответ номер 3, у=9, так как он параллелен оси х
3)5х+3·0 -15=0
5х-15=0
5х=15
х=3 точка А(3;0) -точка пересечения графика с осью ох.
4)6x-7y+12=0 вместо у подставляем нуль и считаем, 6х-7·0 +12=0
6х=-12
х=-2 это и есть абсцисса
В(-2;0) -точка пересечения графика с осью ох.