В задаче отсутствует вопрос. Исхожу из предположения, что требуется определить время движения. t = S/v = 400/v. Но скорость задана не конкретным значением, а границами. Значит время можно только оценить. 50<v<80 заменим обратными числами,при этом меняем знак неравенства. 1/50 > 1/v > 1/80. Запишем в привычном виде: 1/80 < 1/v < 1/50. Теперь умножим все части неравенства на 400. 400/80< 400/v< 400/50. 5< t<8. Значит при заданных условиях время движения от 5 до 8 часов.
Объяснение:
х км/ч - скорость катера в стоячей воде;
(x-2) км/ч - скорость катера против течения;
(x+2) км/ч - скорость катера по течению;
20/(x+2) ч - время, пройденное по течению;
8/(x-2) ч - время, пройденное против течения.
На весь путь катер затратил 2 часа, составим уравнение
Домножив обе части уравнения на 0.5(x+2)(x-2), получаем
10(x-2) + 4(x+2) = (x+2)(x-2)
10x - 20 + 4x + 8 = x² - 4
x² - 14x + 8 = 0
D = 14² - 4 * 1 * 8 = 164
Корень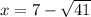 не удовлетворяет условию.
не удовлетворяет условию.