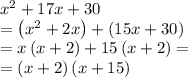
Объяснение:
В знаменателе с точностью до какого-то коэффициента u должен стоять косинус суммы:
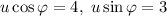
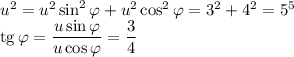
u можно взять положительным, тогда u = 5;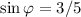 
, 
. Можно было бы взять и отрицательным, при этом были бы другие знаки у синуса и косинуса.
φ тоже можно взять любым, лишь бы у синуса и косинуса были нужные знаки (если u > 0, и то и то будет положительным) и тангенс был равен найденному значению. Я возьму 
, это угол первой четверти.
В числителе должно стоять
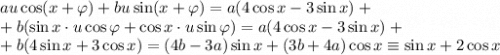
Приравниваем коэффициенты и решаем получившуюся систему:
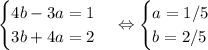
Диаграмма Венна (также используется название диаграмма Эйлера — Венна) — схематичное изображение всех возможных отношений (объединение, пересечение, разность, симметрическая разность) нескольких (часто — трёх) подмножеств универсального множества. На диаграммах Венна универсальное множество {\displaystyle U} изображается множеством точек некоторого прямоугольника, в котором располагаются в виде кругов или других простых фигур все остальные рассматриваемые множества[1][2].

Диаграмма Венна, показывающая все пересечения греческого, русского и латинского алфавитов (буквы заглавные)
Диаграммы Венна применяются при решении задач вывода логических следствий из посылок, выразимых на языке формул классического исчисления высказываний и классического исчисления одноместных предикатов[3], для :
