Кустов красной смородины - 6 штук.
Кустов черной смородины - 9 штук.
Объяснение:
Возьмём количество кустов черной смородины как x; а количество кустов красной смородины как y.
Всего кустов 15 штук, то есть 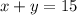 ; также мы знаем, что с кустов собрали ягоды, и их сумма = 51кг, то есть
; также мы знаем, что с кустов собрали ягоды, и их сумма = 51кг, то есть 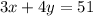 .
.
Получим систему уравнений:
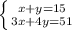
Выразим  через
через 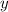 :
:
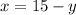
Подставим это значение вместо  во втором уравнении, получим:
во втором уравнении, получим:
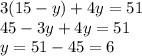
Кустов красной смородины - 6 штук.
Следовательно, кустов черной смородины - 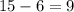 штук.
штук.
Решить уравнение методом введения новой переменной
x/(x²-2)+6*(x²-2)/x = 7
ответ: { - 4/3 , - 1 , 3/2 , 2 } * * * { -1 1/3 ; - 1 ; 1,5 ; 2 } * * *
Объяснение: x/(x²-2)+6*(x²-2)/x =7
ОДЗ: { x≠0 ; x²-2≠ 0 . ⇔ x≠ { -√2 ; 0; √2 }
замена: t =x/(x²-2)
t + 6 /t =7 || t≠0 || ⇔t² -7t + 6=0 ⇒ t₁ =1 ,t₂= 6 ( По теореме Виета )
Обратная замена
а) x/(x²-2) =1 ⇔ x= x²-2 ⇔x²-x-2 =0 ⇒ x₁ = - 1 , x₂= 2 ;
б) x/(x²-2) =6 ⇔ 6x² - x - 12 =0 D = 1² -4*6*(-12)=289 =17²
x₃,₄ =(1 ±17) /( 2*6) x₃ =(1-17)/12 = - 4/3 , x₄ = 3/2.
Пусть количество черной смородины - х кустов, а красной - у кустов. Тогда из условия следует первое равенство:
х+у=15.
Тогда известно, что из черной собираем по 3 кг, а с красной по 4 кг. И суммарно 51 кг -> 3х+4у=51
Решим систему уравнений:
x+y=15
3x+4y=51
x=15-y
3*(15-y)+4y=51
45+y=51
y=6
тогда х=9
Следовательно, кустов черной смородины было 9 кустов, а красной - 6 кустов.
Отв. 6 кустов, 9 кустов