Функция не имеет промежутков убывания
Объяснение:
По теореме если угловой коэффициент прямой меньше нуля, то функция убывает, а если угловой коэффициент прямой больше нуля, то функция возрастает.
Докажем теорему
Рассмотрим функцию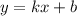 
.Где x,y - переменные; k,b - параметры. Продифференцируем функцию y.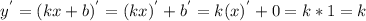
По теореме если производная больше нуля на промежутке M, то на этом промежутке функция возрастает.
По теореме если производная меньше нуля на промежутке M, то на этом промежутке функция убывает.
Тогда согласно теоремам:
если k < 0, то функция убывает.
если k > 0, то функция возрастает.
y=2x − 4 ⇒ k > 0, тогда функция возрастает при x є R.
Объяснение:
((a+7)\(a-7)-(a-7)\(a+7))\(14\(a^2-7a))
Приведем дроби в скобке к общему знаменателю a^2-49, домножив первую дробь на (a+7), а вторую на (a-7):
((a+7)^2-(a-7)^2)\(a^2-49)
По формуле разности квадратов:
((a+7-a+7)(a+7+a-7))\(a^2-49)
14*2a\a^2-49
28a\a^2-49
Представим деление одной дроби на другую умножением первой на перевернутую вторую:
(28a*(a^2-7a))\(14*(a^-49))
Вынесем в числителе "а" за скобку, а в знаменателе разложим скобку на множители:
(28a^2*(a-7))\(14(a-7)(a+7))
Сократим дробь:
2a^2\(x+7)