1) Значение функции - это значение у, а значение аргумента - значение х. Подставляем данные в формулу, считаем (рис.1)
2) Функция y=-2x+5 это линейная функция, а значит графиком для неё будет являться прямая. Чтобы построить график, берем два любых значений Х и подставляем их в формулу, находим У. Полученные точки (это 5 и 3) отмечает на координатной плоскости, проводим через них прямую, получаем наш график. По графику находим, что при х=-0,5 у=6. (рис.2)
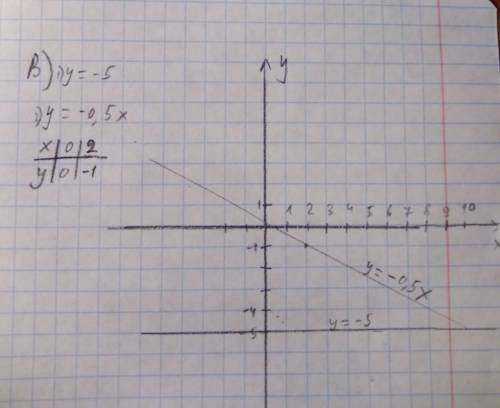
3) Графиком функции y=-5 будет являться прямая, проходящая через -5 оси У и параллельная оси Х. График функции у=-0,5х строим аналогичным образом, что и во 2 номере.
Надеюсь, что
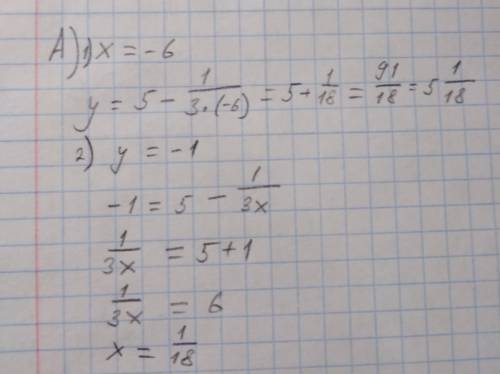

y = [x] - наибольшее целое число, не превосходящее x
y = {x} ≡ x - [x] - дробная часть x
График функции y = [x] - набор ступенек, y = n, если n <= x < n + 1 . График y = [x] + 4 - тот же график, но сдвинутый на 4 единицы вверх.
График функции y = {x} на полуинтервале [0, 1) совпадает с y = x, а дальше повторяется с периодом 1. y = {x + 2} ничем не отличается, так как прибавление целого числа никак не меняется дробную часть. Можно понять это и по-другому: y = {x + 2} это график y = {x}, сдвинутый на 2 единицы влево, но так как функция периодична с периодом 1, ничего не изменится.