(3x-2)x² - 2x(3x-2) + 8(2-3x) = 0
(3x-2)x² - 2x(3x-2) - 8(3x-2)=0
Вынесем за скобку (3х-2).
(3х-2)(х² - 2х - 8) = 0
Разложим на множители второй многочлен (х² - 2х - 8), для этого решим уравнение:
х² - 2х - 8 = 0
D = b - 4ac
D = 4 - 4·1·(-8) = 36
√D = √36 = 6
х₁ = (2+6)/2 = 4
х₂ = (2-6)/2 = - 2
Получим
х² - 2х - 8 = (х-4)(х+2)
Теперь данное уравнение (3х-2)(х² - 2х - 8) = 0 примет вид:
(3х-2)(х-4)(х+2) = 0
Каждую скобку приравняем к нулю и получим корни уравнения.
3х - 2 = 0
х₁ = ²/₃
х - 4 = 0
х₂ = 4
х + 2 = 0
х₃ = - 2
ответ: х₁ = ²/₃; х₂ = 4; х₃ = - 2
Объяснение:
Заметим, что, если дробь имеет ненулевую целую часть, то так зачеркнуть не удастся. Тогда целая часть равна 0. Пусть дробь имеет вид 0,xa - где x - цифра десятков, a - остальные цифры.
Пусть a состоит из n цифр. Тогда запишем уравнение согласно условию:
Пусть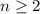
, тогда 
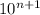делится на 40. В результате получаем 
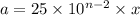, поэтому 
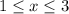, откуда получаем оставшиеся решения: 0,125, 0,25, 0,375.
ответ: 0,125
0,25
0,375