Контрольная работа № 7 «Квадратичная функция»
Вариант I
1. Определите (не строя), какие точки принадлежат графику функции у=х2:
А (3;-9), В (1;1), С (-1;-1), D(-3;9).?
2. Найти координаты вершины параболы:
а) у= х2-4х+5;
б) у= 2х2-7х+9.
3. Найти координаты точек пересечения функции с осями координат
1) у= х2-5х+1
2) у= -2х2+3х+2.
4. Постройте график функции:
1) у= х2-6х+5
2) у= -0,5х2+2х+1.

👇

Открыть все ответы

Ответ:

yrarissikhin

18.02.2021

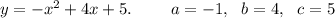
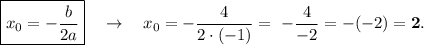
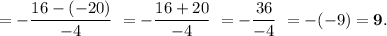
1 ) Формула параболы y=ax2+bx+c,
если а>0 то ветви параболы направленны вверх,
а<0 то ветви параболы направлены вниз.
Свободный член c эта точке пересекается параболы с осью OY;

2 ) Вершина параболы, ее находят по формуле x=(-b)/2a, найденный x подставляем в уравнение параболы и находим y;

3) Нули функции или по другому точки пересечения параболы с осью OX они еще называются корнями уравнения. Чтобы найти корни мы уравнение приравниваем к 0 ax2+bx+c=0;

Виды уравнений:

     a) Полное квадратное уравнение имеет вид ax2+bx+c=0 и решается по дискриминанту;
     b) Неполное квадратное уравнение вида ax2+bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0:
        ax2+bx=0,
        х(ax+b)=0,
        х=0 и ax+b=0;
     c)Неполное квадратное уравнение вида ax2+c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a);

Как решать квадратные уравнения посмотреть тут.

4) Найти несколько дополнительных точек для построения функции.

ПРАКТИЧЕСКАЯ ЧАСТЬ

И так теперь на примере разберем все по действиям:
Пример №1:
y=x2+4x+3
c=3 значит парабола пересекает OY в точке х=0 у=3. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=4 c=3 x=(-b)/2a=(-4)/(2*1)=-2 y= (-2)2+4*(-2)+3=4-8+3=-1 вершина находится в точке (-2;-1)
Найдем корни уравнения x2+4x+3=0
По дискриминанту находим корни
a=1 b=4 c=3
D=b2-4ac=16-12=4
x=(-b±√(D))/2a
x1=(-4+2)/2=-1
x2=(-4-2)/2=-3

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=-2

х -4 -3 -1 0
у 3 0 0 3

Подставляем вместо х в уравнение y=x2+4x+3 значения
y=(-4)2+4*(-4)+3=16-16+3=3
y=(-3)2+4*(-3)+3=9-12+3=0
y=(-1)2+4*(-1)+3=1-4+3=0
y=(0)2+4*(0)+3=0-0+3=3
Видно по значениям функции,что парабола симметрична относительно прямой х=-2

Пример №2:
y=-x2+4x
c=0 значит парабола пересекает OY в точке х=0 у=0. Ветви параболы смотрят вниз так как а=-1 -1<0. a=-1 b=4 c=0 x=(-b)/2a=(-4)/(2*(-1))=2 y=-(2)2+4*2=-4+8=4 вершина находится в точке (2;4)
Найдем корни уравнения -x2+4x=0
Неполное квадратное уравнение вида ax2+bx=0. Чтобы его решить нужно вынести х за скобки, потом каждый множитель приравнять к 0.
х(-x+4)=0, х=0 и x=4.

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=2
х 0 1 3 4
у 0 3 3 0
Подставляем вместо х в уравнение y=-x2+4x значения
y=02+4*0=0
y=-(1)2+4*1=-1+4=3
y=-(3)2+4*3=-9+13=3
y=-(4)2+4*4=-16+16=0
Видно по значениям функции,что парабола симметрична относительно прямой х=2

Пример №3
y=x2-4
c=4 значит парабола пересекает OY в точке х=0 у=4. Ветви параболы смотрят вверх так как а=1 1>0.
a=1 b=0 c=-4 x=(-b)/2a=0/(2*(1))=0 y=(0)2-4=-4 вершина находится в точке (0;-4)
Найдем корни уравнения x2-4=0
Неполное квадратное уравнение вида ax2 +c=0. Чтобы его решить нужно неизвестные перенести в одну сторону, а известные в другую. x =±√(c/a)
x2=4
x1=2
x2=-2

Возьмем несколько произвольных точек, которые находятся рядом с вершиной х=0
х -2 -1 1 2
у 0 -3 -3 0
Подставляем вместо х в уравнение y= x2-4 значения
y=(-2)2-4=4-4=0
y=(-1)2-4=1-4=-3
y=12-4=1-4=-3
y=22-4=4-4=0
Видно по значениям функции,что парабола симметрична относительно прямой х=0

4,4(21 оценок)

Ответ:

toshamilgis

18.02.2021

Это квадратичная функция.

График — парабола, ветви направлены вниз (a = -1), получена из графика y=-x², сдвигом на 2 вправо (по оси X) и на 9 вверх.

ХОД РЕШЕНИЯ:

1) Выпишем коэффициенты.
$y = -x^2+4x+5. \ \ \ \ \ \ \ a=-1, \ \ b=4, \ \ c=5$

2) Найдем начало координат (то есть то место, откуда начинается парабола после сдвига — вершину):

$\boxed{x_0 = - \dfrac{b}{2a}} \ \ \ \rightarrow \ \ \ x_0 = - \dfrac{4}{2\cdot(-1)} = \ - \dfrac{4}{-2} = -(-2) = \boldsymbol{2}.$

$\boxed{y_0 = - \dfrac{b^2-4ac}{4a}} \ \ \ \rightarrow \ \ \ y_0 =- \dfrac{4^2-4\cdot(-1)\cdot5}{4\cdot(-1)} \ =- \dfrac{16-(-20)}{-4}=$

$= - \dfrac{16-(-20)}{-4} \ = - \dfrac{16+20}{-4} \ = - \dfrac{36}{-4} \ = -(-9) = \boldsymbol{9}.$

4) Значит, парабола сдвинется на 2 единичных отрезка вправо (по оси X) и на 9 единичных отрезков вверх (по оси Y). ⇒ О₁(2;9).

Внимание! Строим график функции не y=-x²+4x+5, а y=-x².
Берем стандартные значения, и по ним строим график:
x = 0, y = 0
x = 1, y = -1
x = 2, y = -4.

График в приложении. Желаю успехов!
Постройте график функции y=-x²+4x+5