с алгеброй 7 класс ^2 - это степень / - это дробная черта
Вычислите значение выражения:
(5x-15y)/(9y^2- 6xy+ x^2 ), если х – 3у = 2.
Сократите дробь:
(ac-2bc+2b-a)/(a^2- 4ab+4b^2 ).
Представьте выражение в виде многочлена:
(х2 + 1) (х2 – 1) + х4.
Сократите дробь:
(x^3- 1000z^3)/(x^2- 100z^2 ).
Сократите дробь:
(3x^3- 81)/(2x^2+ 6x+18).
Придумайте уравнение, имеющее ровно два корня; ровно три корня; ровно четыре корня.
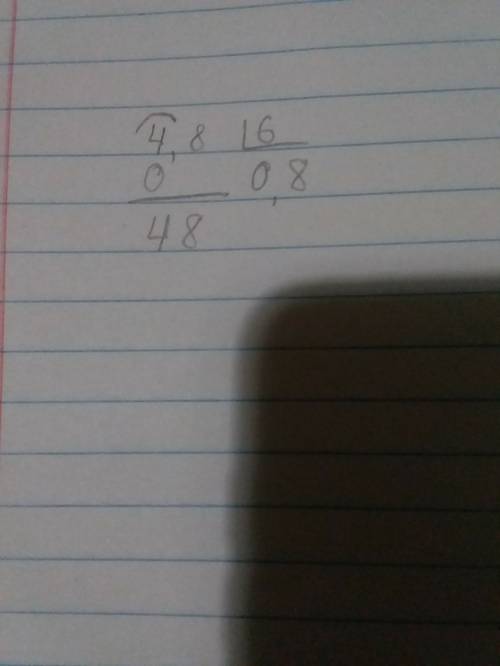
18 - (x - 5) * (x - 4) = -2;
18 - (x^2 - 4 * x - 5 * x + 20) = -2;
18 - (x^2 - 9 * x + 20) = -2;
Так как, перед скобками стоит знак минус, то значения знаков меняются на противоположный знак.
18 - x^2 + 9 * x - 20 = -2;
-x^2 + 9 * x - 2 = -2;
-x^2 + 9 * x - 2 + 2 = 0;
-x^2 + 9 * x = 0;
x^2 - 9 * x = 0;
Найдем дискриминант квадратного уравнения:
D = b2 - 4 * a * c = (-9)2 - 4 * 1 * 0 = 81 - 0 = 81;
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x1 = (9 - √81)/(2 * 1) = (9 - 9)/2 = 0/2 = 0;
x2 = (9 + √81)/(2 * 1) = (9 + 9)/2 = 18/2 = 9;
ответ: х = 0 и х = 9.