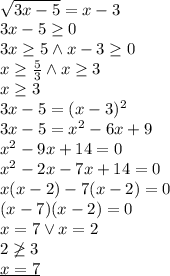
возведем обе части неравенства в квадрат
3x-5=x^2-6x+9
x^2-9x+14=0
x1= 7 x2=2
В уравнениях такого вида надо или делать проверку или накладывать условие на х.
1)3x-5>=0, x>=5/3
x-3>=0, x>=3
Общее решение x>=3, значит х=2 посторонний корень
2)При подстановке в уравнение х=2 видно, что правая часть отрицательна, что невозможно, так как левая часть неотрицательна.
ответ х=7
(0;0), (3·√2; 3/√2); (-3·√2; -3/√2); (3/√2;3·√2); (-3/√2;-3·√2)
Объяснение:
x⁴y+xy⁴=3(x+y)³
xy(x³+y³)=3(x+y)³
xy(x+y)(x²-xy+y²)=3(x+y)³
1) x+y=0⇒y=-x
x³y+xy³=5(x+y)²
x³(-x)+x(-x)³=0
-2x⁴=0
x=y=0
2) x+y≠0, x≠0, y≠0
xy(x+y)(x²-xy+y²)=3(x+y)³
xy(x²-xy+y²)=3(x+y)²
(x²-xy+y²)/3=(x+y)²/(xy)
x³y+xy³=5(x+y)²
xy(x²+y²)=5(x+y)²
(x²+y²)/5=(x+y)²/(xy)
(x²-xy+y²)/3=(x²+y²)/5
5(x²-xy+y²)=3(x²+y²)
2x²-5xy+2y²=0
2x²-4xy-xy+2y²=0
2x(x-2y)-y(x-2y)=0
(x-2y)(2x-y)=0
a) x-2y=0
x=2y
x³y+xy³=5(x+y)²
(2y)³y+2yy³=5(2y+y)²
8y⁴+2y⁴=45y²
10y⁴-45y²=0
2y⁴-9y²=0
y²(2y²-9)=0
2y²-9=0
2y²=9
y²=9/2
y=±3/√2
x=2y=2·(±3)/√2=±3·√2
b) 2x-y=0
y=2x
Аналогично а)
x=±3/√2
y=2y=2·(±3)/√2=±3·√2
Объяснение:
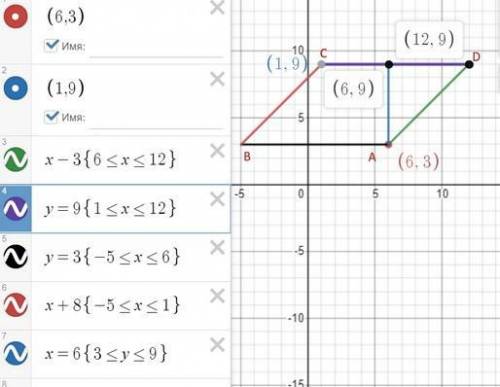
тут главное нарисовать этот параллелограмм
а потом, по координатам точек можно найти АЕ, и сторону CD
а потом и площадь.
сначала откладываем точки А(6; 3) и С (1,9)
потом проводим прямую AD y=x+3
и прямую DC ║ оси ох, это будет прямая у = 9, поскольку она проходит через точку С(1,9) и ║ оси ох и получим точку D(12;9)
(я еще достроила две стороны ВА (у=3) и ВС (у=х+8) - но это не особенно нужно для расчета высоты и площади, просто для наглядности я построила весь параллелограмм)
и потом проводим высоту h, это прямая х = 6 ║ оси оу
вот, собственно, и все
из чертежа понятно, что высота р = координат по у точки C(6;3) и прямой у = 9, т.е h= 9-3=6
теперь длина CD - это разность координат по х точки С(1; 9) и точки пересечения прямых х+3 и у=9 - это точка D(12;9), т.е CD = 12-1=11
ну вот и площадь
S=h*CD = 6*11=66
на рисунке я, вроде, всё подписала, где какие уравнения и графики.
слева от уравнения в кружке цветом обозначен цвет прямой на графике....